3. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
3.1. Логика проверки
статистических гипотез
Пусть х1,
х2, ..., хп - случайная
выборка значений случайной величины 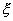 , имеющей некоторое полностью или частично
неизвестное распределение F(x). В
предыдущем разделе рассматривались методы получения оценок параметров или
характеристик этого неизвестного распределения. Однако часто нас интересуют не
столько конкретные количественные оценки, сколько правильность или ошибочность
некоторых утверждений, относящихся к распределению наблюдаемой случайной
величины. Например, является ли это распределение нормальным или нет? Или,
равно математическое ожидание заданному значению или нет? Если кроме выборки х1,
х2, ..., хп имеется
выборка y1, y2, ..., yп значений другой
случайной величины
, имеющей некоторое полностью или частично
неизвестное распределение F(x). В
предыдущем разделе рассматривались методы получения оценок параметров или
характеристик этого неизвестного распределения. Однако часто нас интересуют не
столько конкретные количественные оценки, сколько правильность или ошибочность
некоторых утверждений, относящихся к распределению наблюдаемой случайной
величины. Например, является ли это распределение нормальным или нет? Или,
равно математическое ожидание заданному значению или нет? Если кроме выборки х1,
х2, ..., хп имеется
выборка y1, y2, ..., yп значений другой
случайной величины 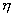 , то можно поставить
вопрос о том, равны или нет математические ожидания случайных величин
, то можно поставить
вопрос о том, равны или нет математические ожидания случайных величин 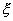 и
и 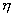 ? Если имеется выборка (х1,
y1), (х2, y2), …, (хп, yп) двумерной случайной величины
? Если имеется выборка (х1,
y1), (х2, y2), …, (хп, yп) двумерной случайной величины 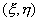 , то может возникнуть
вопрос о том, равен нулю или нет коэффициент корреляции между
, то может возникнуть
вопрос о том, равен нулю или нет коэффициент корреляции между 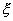 и
и 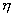 ?
?
Решению задач проверки
гипотез о генеральном распределении по выборке из этого распределения посвящен
специальный раздел математической статистики - проверка статистических гипотез.
Логика проверки гипотез в математической статистике (она напоминает логику
доказательства от противного) состоит в следующем. Вначале предполагается, что
проверяемая гипотеза (ее принято называть нулевой гипотезой и
обозначать H0) верна. В предположении, что H0 верна,
ищется распределение вероятностей некоторой функции g(х1,
х2,...,хп) от
значений выборки, называемой статистикой критерия (правило проверки
гипотезы принято называть критерием), и в области значений этой
статистики выделяется некоторая область W, называемая критической
областью, такая, что вероятность 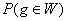 попадания выборочного
значения статистики g в эту область не
превосходит заданного малого значения
попадания выборочного
значения статистики g в эту область не
превосходит заданного малого значения  , называемого уровнем значимости критерия (обычно
полагают
, называемого уровнем значимости критерия (обычно
полагают  равным 0.05 или 0.01).
Если для данной конкретной выборки g попадает в критическую
область W, то гипотеза H0 отвергается
(говорят - "отвергается на уровне значимости
равным 0.05 или 0.01).
Если для данной конкретной выборки g попадает в критическую
область W, то гипотеза H0 отвергается
(говорят - "отвергается на уровне значимости  "), поскольку
вероятность этого события при верной H0 мала. Если же g
не попадает в критическую область W, то говорят, что
"гипотеза H0 не отвергается на уровне
значимости
"), поскольку
вероятность этого события при верной H0 мала. Если же g
не попадает в критическую область W, то говорят, что
"гипотеза H0 не отвергается на уровне
значимости  " (или -
"полученные данные не дают оснований отвергнуть гипотезу H0
на уровне значимости
" (или -
"полученные данные не дают оснований отвергнуть гипотезу H0
на уровне значимости  ").
").
Очевидно, однако, что
можно разными способами задать статистику критерия g(х1,
х2, ..., хп), а для
заданной статистики можно разными способами выбрать критическую область W,
удовлетворяющую условию 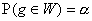 . Поэтому следует
выбирать g и W в некотором смысле
наилучшими из возможных, а именно такими, чтобы полученный критерий был наиболее
мощным.
. Поэтому следует
выбирать g и W в некотором смысле
наилучшими из возможных, а именно такими, чтобы полученный критерий был наиболее
мощным.
Для определения понятия мощности
критерия введем понятие альтернативной гипотезы H1,
т.е. гипотезы, которая выполняется, если не выполняется нулевая гипотеза H0.
Тогда в терминах правильности или ошибочности принятия H0 и H1
можно указать четыре потенциально возможных результата применения
критерия к выборке, представленные в табл. 3. Как мы видим мощность критерия -
это вероятность принятия при применении данного критерия альтернативной
гипотезы H1 при условии, что она верна. Очевидно, что при
фиксированной ошибке 1-го рода (ее мы задаем сами, и она не зависит от свойств
критерия) критерий будет тем лучше, чем больше его мощность (т.е. чем меньше
ошибка 2-го рода).
Таблица 3
|
|
Принята гипотеза
|
|
H0
|
H1
|
|
Верна
Гипотеза
|
H0
|
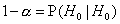 - вероятность
правильно принять H0, когда верна H0 - вероятность
правильно принять H0, когда верна H0
|
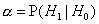
- вероятность ошибочно принять H1, когда верна
H0 (ошибка 1-го рода, уровень значимости)
|
|
H1
|
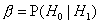
- вероятность ошибочно принять H0, когда верна
H1 (ошибка 2-го рода)
|
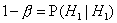
- вероятность правильно принять H1, когда
верна H1 (мощность критерия)
|
Проиллюстрируем основные
понятия рассмотренной методологии на простом примере проверки гипотезы о
равенстве математического ожидания нормально распределенной случайной величины
с известной дисперсией заданному числу (с точки зрения практического применения
этот пример несколько искусственен, поскольку дисперсия наблюдаемой случайной
величины обычно неизвестна).
3.2. Проверка гипотезы о
равенстве заданному числу математического ожидания нормально распределенной
случайной величины с
известной дисперсией
Итак, пусть 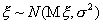 ,
, 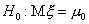 и
и 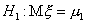 , и пусть имеется выборка х1, х2,
..., хп значений случайной величины
, и пусть имеется выборка х1, х2,
..., хп значений случайной величины 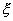 объема n.
Предположим, что H0 верна и выберем в качестве статистики
критерия стандартизованное выборочное среднее
объема n.
Предположим, что H0 верна и выберем в качестве статистики
критерия стандартизованное выборочное среднее
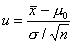
При верной H0
статистика u имеет стандартное
нормальное распределение, 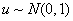 , представленное на рис.
4. На этом рисунке также указана критическая область уровня
, представленное на рис.
4. На этом рисунке также указана критическая область уровня 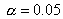 , состоящая из двух
бесконечных полуинтервалов
, состоящая из двух
бесконечных полуинтервалов 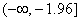 и
и 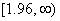 , вероятность попадания в каждый из которых
статистики u равна
, вероятность попадания в каждый из которых
статистики u равна 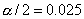 .
.
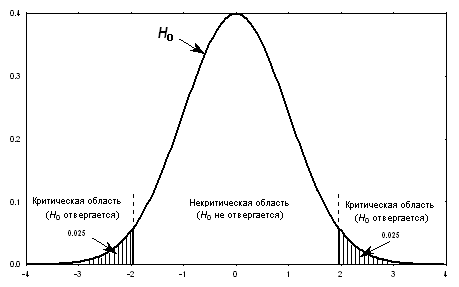
Рис. 4.
Пример критической области.
Имеются формализованные
подходы к выбору статистик критериев и построению критических областей, приводящие
к наиболее мощным критериям, но мы их здесь не рассматриваем. Неформальное же
правило состоит в том, чтобы выбирать в качестве статистики величину,
характеризующую степень отклонения от нулевой гипотезы. Очевидно, разность 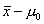 удовлетворяет этому условию, а
деление на константу
удовлетворяет этому условию, а
деление на константу 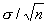 , сохраняя это качество, приводит к
величине u с полностью заданным распределением, что позволяет выбрать
критическую область с требуемым уровнем значимости. Неформальное
правило выбора критической области состоит в том, чтобы она включала
значения статистики, соответствующие наибольшим отклонениям от нулевой гипотезы
- на рис. 4 эта рекомендация соблюдена.
, сохраняя это качество, приводит к
величине u с полностью заданным распределением, что позволяет выбрать
критическую область с требуемым уровнем значимости. Неформальное
правило выбора критической области состоит в том, чтобы она включала
значения статистики, соответствующие наибольшим отклонениям от нулевой гипотезы
- на рис. 4 эта рекомендация соблюдена.
До сих пор мы говорили о свойствах
критерия в предположении, что верна гипотеза H0. А что происходит, когда верна
альтернативная гипотеза H1? В этом случае распределение статистики
критерия u изменится. Чтобы его найти, произведем преобразование
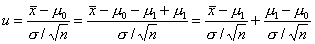
из которого следует, что при гипотезе H1
распределение статистики u отличается от
стандартного нормального сдвигом на величину 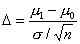 , т.е.
, т.е. 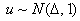 при выполнении H1.
при выполнении H1.
На рис. 5 взаимное
расположение плотностей распределения статистики u при гипотезах H0
и H1 показано для случая 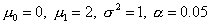 и n=1. Вероятности ошибки
2-го рода
и n=1. Вероятности ошибки
2-го рода 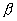 соответствует площадь
под кривой функции плотности при H1 на промежутке от –1.96 до
1.96, где не отвергается гипотеза H0, а следовательно,
ошибочно не принимается гипотеза H1. В данном случае ошибка
2-го рода,
соответствует площадь
под кривой функции плотности при H1 на промежутке от –1.96 до
1.96, где не отвергается гипотеза H0, а следовательно,
ошибочно не принимается гипотеза H1. В данном случае ошибка
2-го рода, 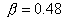 , довольно велика. Это
произошло, главным образом, потому, что мал объем выборки - имеется всего одно
наблюдение, n=1. При увеличении n распределение,
соответствующее альтернативной гипотезе H1, будет сдвигаться
вправо, поскольку величина
, довольно велика. Это
произошло, главным образом, потому, что мал объем выборки - имеется всего одно
наблюдение, n=1. При увеличении n распределение,
соответствующее альтернативной гипотезе H1, будет сдвигаться
вправо, поскольку величина 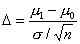 будет увеличиваться, что
приведет, как легко понять по рис. 5, к уменьшению ошибки
будет увеличиваться, что
приведет, как легко понять по рис. 5, к уменьшению ошибки 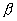 . Очевидно также, что большей величине разности
. Очевидно также, что большей величине разности 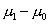 соответствует
большая величина
соответствует
большая величина  , и
следовательно меньшая ошибка 2-го рода. Ошибка 2-го рода уменьшается также при
уменьшении дисперсии
, и
следовательно меньшая ошибка 2-го рода. Ошибка 2-го рода уменьшается также при
уменьшении дисперсии 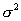 наблюдаемой
случайной величины. Кроме того
наблюдаемой
случайной величины. Кроме того 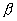 уменьшается при
увеличении
уменьшается при
увеличении 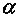 , однако не
принято брать
, однако не
принято брать  больше 0.05. При уменьшении
больше 0.05. При уменьшении  ошибка
ошибка 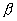 ,
напротив, растет, поэтому не следует брать
,
напротив, растет, поэтому не следует брать  слишком
малым, если число наблюдений n мало, разность между
слишком
малым, если число наблюдений n мало, разность между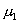 и
и 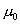 невелика, а дисперсия
невелика, а дисперсия 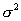 -
большая.
-
большая.
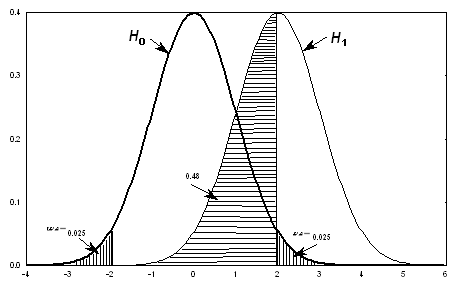
Рис.
5. Взаимосвязь между ошибками 1-го и 2-го рода при двусторонней альтернативе.
Содержательно, ошибка
1-го рода - это ошибка ложного обнаружения несуществующего отклонения от
нулевой гипотезы (ложного обнаружения несуществующего эффекта). Ошибка же 2-го
рода - это ошибка ложного необнаружения существующего
отклонения от нулевой гипотезы (ложного необнаружения
существующего эффекта). Мощность критерия - это его способность обнаружить
имеющееся отклонение от нулевой гипотезы.
В приведенном примере мы
предполагали, что альтернативной гипотезе H1 соответствует
вполне определенное распределение 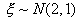 , что позволило нам найти конкретное значение
ошибки 2-го рода. Такого рода альтернативные гипотезы называются простыми
альтернативами. Однако на практике чаще встречается ситуация, когда
конкретной нулевой гипотезе противопоставляется целый спектр альтернатив.
Например,
, что позволило нам найти конкретное значение
ошибки 2-го рода. Такого рода альтернативные гипотезы называются простыми
альтернативами. Однако на практике чаще встречается ситуация, когда
конкретной нулевой гипотезе противопоставляется целый спектр альтернатив.
Например, 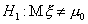 или
или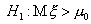 . Такого рода альтернативные гипотезы называются сложными
альтернативами. В случае сложной альтернативной гипотезы мы не можем
определить величину ошибки второго рода. Например, в рассматриваемой ситуации
она может быть значительной даже при очень большом числе наблюдений если
различие между
. Такого рода альтернативные гипотезы называются сложными
альтернативами. В случае сложной альтернативной гипотезы мы не можем
определить величину ошибки второго рода. Например, в рассматриваемой ситуации
она может быть значительной даже при очень большом числе наблюдений если
различие между 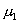 и
и 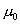 мало. Поэтому в ситуации, когда статистика критерия не
попадает в критическую область, не утверждают категорично, что "нулевая
гипотеза принимается", а формулируют вывод более осторожно: " нулевая
гипотеза не отвергается". Тем самым подчеркивается, что хотя мы и не
обнаружили отклонения от нулевой гипотезы, мы могли его при верной H1
ошибочно не обнаружить с вероятностью
мало. Поэтому в ситуации, когда статистика критерия не
попадает в критическую область, не утверждают категорично, что "нулевая
гипотеза принимается", а формулируют вывод более осторожно: " нулевая
гипотеза не отвергается". Тем самым подчеркивается, что хотя мы и не
обнаружили отклонения от нулевой гипотезы, мы могли его при верной H1
ошибочно не обнаружить с вероятностью 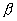 ,
которую мы не знаем и которая, возможно, довольно значительна. Если же ошибка
,
которую мы не знаем и которая, возможно, довольно значительна. Если же ошибка 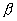 действительно велика, то утверждение "нулевая
гипотеза принимается" не представляет большой ценности. Например, положив
равной нулю ошибку 1-го рода, мы, независимо от результатов наблюдений, всегда
будем принимать гипотезу H0, поскольку критическая область
будет включать всю область определения статистики критерия. Однако при этом
ошибка 2-го рода будет равна единице, т.е. если даже отклонение от нулевой
гипотезы имеется, то мы его с вероятностью единица не обнаружим.
действительно велика, то утверждение "нулевая
гипотеза принимается" не представляет большой ценности. Например, положив
равной нулю ошибку 1-го рода, мы, независимо от результатов наблюдений, всегда
будем принимать гипотезу H0, поскольку критическая область
будет включать всю область определения статистики критерия. Однако при этом
ошибка 2-го рода будет равна единице, т.е. если даже отклонение от нулевой
гипотезы имеется, то мы его с вероятностью единица не обнаружим.
Сложные альтернативы
могут быть двусторонними (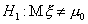 ) и односторонними (
) и односторонними (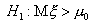 или
или 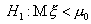 ). Если имеется достоверная информация о направлении
отклонения от нулевой гипотезы, то использование односторонней альтернативы
предпочтительнее двусторонней, поскольку это повышает мощность критерия. Если,
например, известно, что отклонение математического ожидания
). Если имеется достоверная информация о направлении
отклонения от нулевой гипотезы, то использование односторонней альтернативы
предпочтительнее двусторонней, поскольку это повышает мощность критерия. Если,
например, известно, что отклонение математического ожидания 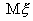 от
гипотетического значения
от
гипотетического значения 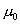 может произойти только в большую сторону, то в
качестве альтернативы следует взять гипотезу
может произойти только в большую сторону, то в
качестве альтернативы следует взять гипотезу 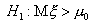 . Критическая область уровня
. Критическая область уровня  в этом случае будет состоять не из двух бесконечных
полуинтервалов
в этом случае будет состоять не из двух бесконечных
полуинтервалов 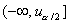 и
и 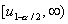 , из одного -
, из одного - 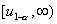 .
.
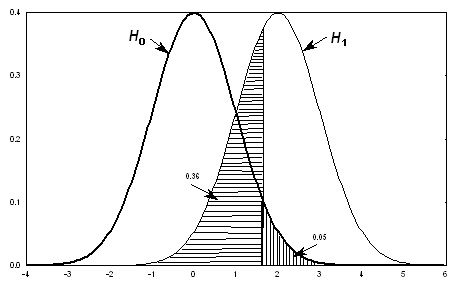
Рис.
6. Взаимосвязь между ошибками 1-го и 2-го рода при односторонней альтернативе.
На рис. 6 ситуация с односторонней
альтернативой представлена для случая 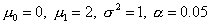 и n=1. Вероятности ошибки
2-го рода
и n=1. Вероятности ошибки
2-го рода 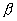 соответствует площадь
под кривой плотности статистики критерия g при условии, что верна
гипотеза H1 на промежутке от
соответствует площадь
под кривой плотности статистики критерия g при условии, что верна
гипотеза H1 на промежутке от 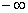 до 1.64.
до 1.64. 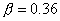 , что
меньше, чем для аналогичной двусторонней альтернативы, представленной на рис. 5
(строго говоря, в ситуации рис. 5 тоже предпочтительнее было бы использовать
альтернативу
, что
меньше, чем для аналогичной двусторонней альтернативы, представленной на рис. 5
(строго говоря, в ситуации рис. 5 тоже предпочтительнее было бы использовать
альтернативу 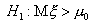 , поскольку направление
отклонения от нулевой гипотезы было известно).
, поскольку направление
отклонения от нулевой гипотезы было известно).
Пример. Известно, что датчик
генерирует случайные числа, нормально распределенные с дисперсией 1, но есть
сомнения в том, что математическое ожидание равно 0. Требуется проверить
гипотезу о равенстве математического ожидания нулю по следующей случайной
выборке объема n=25:
0.830
0.177 -0.294 0.471 -0.044 0.635
2.209 -0.394 -0.404
1.257
1.137 -0.839 1.668 0.751 0.416
-0.922 1.473 -0.317
0.220
0.414 0.428 1.088 -1.130 -0.015
0.142
Выборочное среднее равно
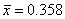 , следовательно, для статистики
критерия получаем
, следовательно, для статистики
критерия получаем
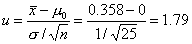
Значение 1.79 не выходит
за двусторонние 5%-ные критические пределы 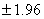 , поэтому гипотеза не отвергается.
, поэтому гипотеза не отвергается.
На самом деле математическое
ожидание датчика было положено равным 0.25, т.е. отклонение ошибочно не было
обнаружено - при проверке гипотезы была сделана ошибка 2-го рода. Очевидно,
мощность критерия при данном числе наблюдений n=25, данной разности между
гипотетическим и истинным математическими ожиданиями 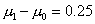 и данной
дисперсии
и данной
дисперсии 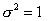 недостаточна.
недостаточна.
В другом эксперименте с этим же
датчиком была получена выборка значений объема n=100. Выборочное среднее
оказалось равным 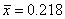 , а значение статистики - равным u=2.18, что дало основание отвергнуть
нулевую гипотезу.
, а значение статистики - равным u=2.18, что дало основание отвергнуть
нулевую гипотезу.
3.3. Проверка гипотезы о
равенстве заданному числу математического ожидания нормально распределенной
случайной величины
с неизвестной дисперсией
(одновыборочный
t-критерий)
Аналогично случаю
построения доверительного интервала для неизвестного математического ожидания
нормально распределенной случайной величины, в случае неизвестной дисперсии мы
возьмем в качестве статистики критерия проверки гипотезы о равенстве
математического ожидания заданному числу ту же статистику, что и в случае с известной
дисперсией, но с заменой неизвестного среднеквадратичного отклонения 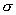 на его выборочную
оценку s
на его выборочную
оценку s
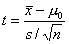
Статистика t
имеет t -распределение с n-1 степенями свободы.
Соответственно, критическая область для проверки гипотезы 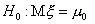 против
двусторонней альтернативы
против
двусторонней альтернативы 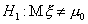 будет состоять из двух бесконечных полуинтервалов
будет состоять из двух бесконечных полуинтервалов 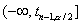 и
и 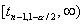 ,
против односторонней альтернативы
,
против односторонней альтернативы 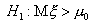 -
из одного полуинтервала
-
из одного полуинтервала 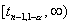 и против
односторонней альтернативы
и против
односторонней альтернативы 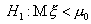 - также из
одного полуинтервала
- также из
одного полуинтервала 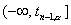 , где
, где 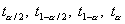 обозначают квантили t-распределения
с n-1 степенями свободы соответствующего уровня
значимости (в силу симметричности t-распределения
справедливы равенства
обозначают квантили t-распределения
с n-1 степенями свободы соответствующего уровня
значимости (в силу симметричности t-распределения
справедливы равенства 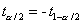 и
и 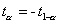 ).
).
Пример. Рассмотрим пример
предыдущего параграфа с 25 случайными числами в предположении, что дисперсия
неизвестна. В этом случае необходимо вычислить оценку среднеквадратичного
отклонения, которая оказывается равной s=0.830. Выборочное
значение статистики критерия, соответственно, равно
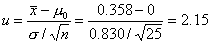
Это значение должно быть
сравнено с 5%-ными двусторонними критическими пределами, равными 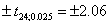 . Выборочное значение статистики
выходит за эти пределы, следовательно, гипотеза о равенстве математического
ожидания нулю должна быть отвергнута на уровне значимости 5%.
. Выборочное значение статистики
выходит за эти пределы, следовательно, гипотеза о равенстве математического
ожидания нулю должна быть отвергнута на уровне значимости 5%.
Заметим, что хотя применение t-критерия требует нормальности
исходной случайной величины, он может применяться и при умеренных отклонениях
от нормальности и не слишком малых n 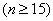 .
.
3.4. Проверка гипотезы о
равенстве заданному числу дисперсии нормально распределенной случайной величины
(одновыборочный c2-критерий)
Для проверки гипотезы 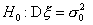 о равенстве дисперсии
о равенстве дисперсии 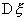 нормально
распределенной случайной величины
нормально
распределенной случайной величины 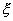 заданному числу
заданному числу 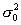 рекомендуется
использовать статистику
рекомендуется
использовать статистику
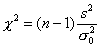
Можно показать, что эта
статистика при условии, что верна гипотеза H0, распределена
по закону c2 с п-1 степенями свободы. Критическая область уровня  при двусторонней
альтернативе
при двусторонней
альтернативе 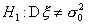 состоит из двух
промежутков:
состоит из двух
промежутков: 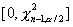 и
и 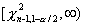 , где
, где 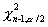 и
и
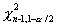 -
квантили порядка
-
квантили порядка 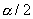 и
и 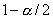 распределения
распределения 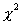 с
п-1 степенями свободы. Для односторонней альтернативы
с
п-1 степенями свободы. Для односторонней альтернативы 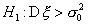 критическая
область имеет вид
критическая
область имеет вид 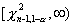 , а для
альтернативы
, а для
альтернативы 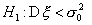 -
соответственно,
-
соответственно, 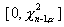 .
.
3.5. Проверка гипотезы о
равенстве математических ожиданий двух независимых нормально распределенных
случайных величин (двухвыборочный t-критерий)
Предположим, что имеются
случайные выборки х1, х2, ..., хп и y1, y2, ..., ym значений двух
независимых нормально распределенных случайных величин 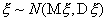 и
и 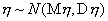 и требуется
проверить гипотезу
и требуется
проверить гипотезу 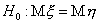 о равенстве математических
ожиданий этих случайных величин.
о равенстве математических
ожиданий этих случайных величин.
(а) Если известно, что
дисперсии случайных величин x и h равны, 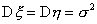 (значение
(значение 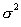 неизвестно), то можно получить следующую объединенную несмещенную
оценку для
неизвестно), то можно получить следующую объединенную несмещенную
оценку для 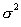
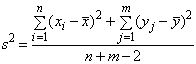
В этом случае s2/n и s2/m
будут несмещенными оценками для дисперсии выборочных средних 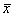 и
и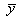 , а сумма s2/n+s2/m - несмещенной оценкой для дисперсии разности средних
, а сумма s2/n+s2/m - несмещенной оценкой для дисперсии разности средних 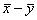 . Соответственно, статистика
. Соответственно, статистика
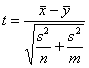
как можно показать, будет иметь t-распределение
с n+m-2 степенями свободы.
Критическая область уровня  для проверки гипотезы
для проверки гипотезы 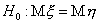 против двусторонней
альтернативы
против двусторонней
альтернативы 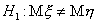 будет состоять из двух бесконечных
полуинтервалов
будет состоять из двух бесконечных
полуинтервалов 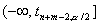 и
и 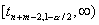 , против односторонней
альтернативы
, против односторонней
альтернативы 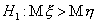 - из полуинтервала
- из полуинтервала
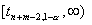 и против
альтернативы
и против
альтернативы 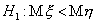 - из полуинтервала
- из полуинтервала
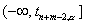 , где
, где 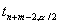 ,
, 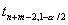 ,
, 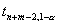 ,
, 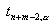 обозначают
соответствующие квантили t-распределения с n+m-2 степенями
свободы.
обозначают
соответствующие квантили t-распределения с n+m-2 степенями
свободы.
(б) Если нет оснований
считать, что дисперсии случайных величин x и h равны, то для каждой из дисперсий 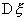 и
и 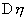 вычисляется своя
оценка
вычисляется своя
оценка

и соответственно модифицируется статистика
критерия
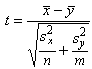
которая, как можно показать, имеет t-распределение
с числом степеней свободы, равным целой части от 1/k, где k
выражается следующей формулой
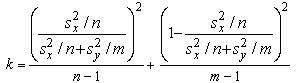
3.6. Проверка гипотезы о
равенстве дисперсий двух независимых нормально распределенных случайных величин
(двухвыборочный
F-критерий)
В предыдущем параграфе
мы видели, что процедура проверки гипотезы о равенстве двух математических
ожиданий двух нормально распределенных случайных величин упрощается, если
их дисперсии одинаковы. Следующий критерий позволяет проверить нулевую
гипотезу 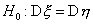 о равенстве
дисперсий двух нормально распределенных случайных величин. В качестве
статистики критерия используется отношение несмещенных оценок дисперсий этих
случайных величин
о равенстве
дисперсий двух нормально распределенных случайных величин. В качестве
статистики критерия используется отношение несмещенных оценок дисперсий этих
случайных величин
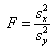
При условии, что верна
гипотеза H0, можно доказать, что статистика критерия
имеет F-распределение с n-1 и m-1 степенями свободы.
Соответственно, критическая область уровня  для проверки гипотезы
для проверки гипотезы 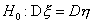 против двусторонней
альтернативы
против двусторонней
альтернативы 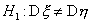 будет состоять из двух промежутков:
будет состоять из двух промежутков: 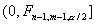 и
и 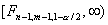 , где
, где 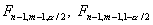 - квантили порядка
- квантили порядка 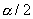 и
и 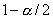 F-распределения
с n-1 и m-1 степенями свободы. Для односторонней альтернативы
F-распределения
с n-1 и m-1 степенями свободы. Для односторонней альтернативы 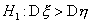 критическая
область имеет вид
критическая
область имеет вид 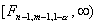 , а для
альтернативы
, а для
альтернативы 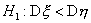 - соответственно
- соответственно 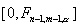 . Если в качестве статистики использовать отношение большей
оценки дисперсии к меньшей, то в качестве критической области при двусторонней
альтернативе используется односторонняя критическая область
. Если в качестве статистики использовать отношение большей
оценки дисперсии к меньшей, то в качестве критической области при двусторонней
альтернативе используется односторонняя критическая область 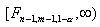 -
это позволяет ограничиться таблицами F-распределения, содержащими значения функции распределения
только для аргументов больших единицы.
-
это позволяет ограничиться таблицами F-распределения, содержащими значения функции распределения
только для аргументов больших единицы.
Заметим, что в отличие
от t-критерия F-критерий чувствителен к
отклонениям исходных случайных величин от нормальности. При значительных
отклонениях от нормальности, особенно при небольшом числе наблюдений его не
следует применять.
3.7. Приближенный
критерий для проверки гипотезы о равенстве параметров двух независимых
биномиальных случайных величин (критерий для сравнения двух вероятностей)
Пусть две независимые биномиально распределенные случайные величины 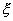 и
и 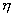 с параметрами п,
с параметрами п, 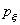 и m,
и m, 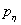 , соответственно, при
проведении независимых испытаний приняли значения k и l. Требуется проверить гипотезу
, соответственно, при
проведении независимых испытаний приняли значения k и l. Требуется проверить гипотезу 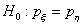 о
равенстве параметров
о
равенстве параметров 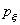 и
и 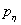 . Для этого можно использовать статистику
. Для этого можно использовать статистику
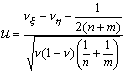
где 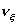 ,
, 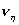 и
и 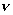 - выборочные частоты, вычисленные по
первой, второй и объединенной выборкам:
- выборочные частоты, вычисленные по
первой, второй и объединенной выборкам: 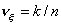 ,
, 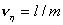 и
и 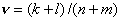 . Если верна гипотеза H0,
то для
. Если верна гипотеза H0,
то для 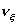 ,
, 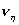 , не очень близких к 0
или 1, и при достаточно больших п, m эта статистика имеет приближенно стандартное нормальное
распределение. Практически приближение применимо, если каждая из четырех
численностей k, l, n-k и m-l больше пяти.
, не очень близких к 0
или 1, и при достаточно больших п, m эта статистика имеет приближенно стандартное нормальное
распределение. Практически приближение применимо, если каждая из четырех
численностей k, l, n-k и m-l больше пяти.
Критическая область
уровня значимости  для
проверки гипотезы
для
проверки гипотезы 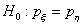 против двусторонней альтернативы
против двусторонней альтернативы 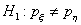 будет состоять из двух бесконечных полуинтервалов
будет состоять из двух бесконечных полуинтервалов 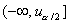 и
и 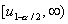 ,
против односторонней альтернативы
,
против односторонней альтернативы 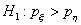 -
из одного полуинтервала
-
из одного полуинтервала 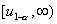 и против
односторонней альтернативы
и против
односторонней альтернативы 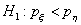 - также из
одного полуинтервала
- также из
одного полуинтервала 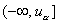 , где
, где 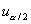 ,
, 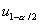 ,
, 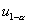 , и
, и 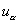 обозначают
квантили соответствующего порядка стандартного нормального распределения.
обозначают
квантили соответствующего порядка стандартного нормального распределения.
Имеется также точный
критерий для проверки этой гипотезы (см., напр., [3]).
3.8. Приближенный
критерий для проверки гипотезы
о равенстве параметров
двух независимых
пуассоновских случайных
величин
Пусть две независимые
случайные величины 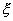 и
и 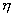 , имеющие пуассоновское распределение с параметрами
, имеющие пуассоновское распределение с параметрами 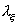 и
и
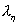 , соответственно, при проведении испытаний приняли значения
k и l. Требуется
проверить гипотезу
, соответственно, при проведении испытаний приняли значения
k и l. Требуется
проверить гипотезу 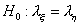 о
равенстве параметров
о
равенстве параметров 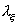 и
и 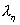 распределений этих
случайных величин. Для этого можно использовать
статистику
распределений этих
случайных величин. Для этого можно использовать
статистику
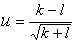
распределение которой при выполнении H0 и при k+l>5 довольно точно приближается стандартным нормальным
распределением. Соответственно, как и в предыдущем параграфе, критическая
область уровня значимости  для
проверки гипотезы
для
проверки гипотезы 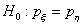 против двусторонней альтернативы
против двусторонней альтернативы 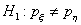 будет состоять из двух бесконечных полуинтервалов
будет состоять из двух бесконечных полуинтервалов 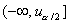 и
и 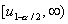 ,
против односторонней альтернативы
,
против односторонней альтернативы 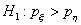 -
из одного полуинтервала
-
из одного полуинтервала 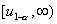 и против
односторонней альтернативы
и против
односторонней альтернативы 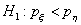 - также из
одного полуинтервала
- также из
одного полуинтервала 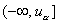 .
.
3.9. Приближенный
критерий для проверки гипотезы о равенстве нулю коэффициента корреляции между
компонентами двумерной нормально распределенной случайной величины
Пусть (х1,
y1), (х2, y2), …, (хп, yп) - случайная выборка
пар значений двумерной случайной величины 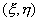 , имеющей двумерное нормальное
распределение. Требуется проверить гипотезу
, имеющей двумерное нормальное
распределение. Требуется проверить гипотезу 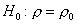 о равенстве коэффициента корреляции
о равенстве коэффициента корреляции 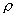 этого
двумерного распределения заданному числу
этого
двумерного распределения заданному числу 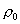 . Для проверки этой гипотезы можно использовать статистику
. Для проверки этой гипотезы можно использовать статистику
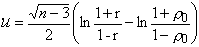
распределение которой при выполнении H0 и при достаточно большом n довольно точно
приближается стандартным нормальным распределением. Соответственно, как и в
предыдущих двух параграфах, критическая область уровня значимости  для
проверки гипотезы
для
проверки гипотезы 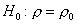 против
двусторонней альтернативы
против
двусторонней альтернативы 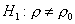 будет
состоять из двух бесконечных полуинтервалов
будет
состоять из двух бесконечных полуинтервалов 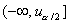 и
и 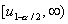 ,
против односторонней альтернативы
,
против односторонней альтернативы 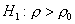 -
из одного полуинтервала
-
из одного полуинтервала 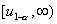 и против
односторонней альтернативы
и против
односторонней альтернативы 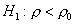 - также из
одного полуинтервала
- также из
одного полуинтервала 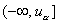 .
.
Обычно проверяется
гипотеза о равенстве коэффициента корреляции нулю, что в случае двумерного нормального распределения, как ранее отмечалось, эквивалентно проверке
гипотезы о независимости 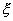 и
и 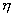 . В этом случае
приведенное выше выражение для статистики критерия упрощается
. В этом случае
приведенное выше выражение для статистики критерия упрощается
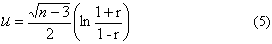
Пример. Пусть объем выборки n=10,
вычисленное по выборке значение r=0.6 и требуется
проверить гипотезу 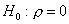 против альтернативы
против альтернативы 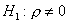 .
.
Выборочное значение статистики u, вычисленное по формуле (5), равно
1.83. Поскольку оно не выходит за двусторонние 5%-ные критические пределы
стандартного нормального распределения 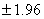 , то у нас нет оснований
отвергнуть нулевую гипотезу об отсутствии корреляции. Если бы у нас были
основания предполагать, что корреляционная зависимость в случае ее наличия
может быть только положительной, то следовало бы использовать для проверки H0, одностороннюю
критическую область, которая для
, то у нас нет оснований
отвергнуть нулевую гипотезу об отсутствии корреляции. Если бы у нас были
основания предполагать, что корреляционная зависимость в случае ее наличия
может быть только положительной, то следовало бы использовать для проверки H0, одностороннюю
критическую область, которая для 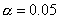 представляет собой бесконечный полуинтервал
представляет собой бесконечный полуинтервал 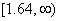 .
Значение 1.83 попадает в эту критическую область и, следовательно, гипотеза об
отсутствии корреляции должна бы была быть отвергнута. Заметим, однако, что
число наблюдений в данном примере недостаточно велико для уверенного
использования данного приближенного критерия. Если к этому добавить тот факт,
что выборочное значение статистики критерия находится вблизи границы
критической области, то следует заключить, что по имеющимся данным нельзя
сделать надежного вывода ни о наличии, ни об отсутствии корреляции.
.
Значение 1.83 попадает в эту критическую область и, следовательно, гипотеза об
отсутствии корреляции должна бы была быть отвергнута. Заметим, однако, что
число наблюдений в данном примере недостаточно велико для уверенного
использования данного приближенного критерия. Если к этому добавить тот факт,
что выборочное значение статистики критерия находится вблизи границы
критической области, то следует заключить, что по имеющимся данным нельзя
сделать надежного вывода ни о наличии, ни об отсутствии корреляции.
Отметим, что если бы, скажем,
значение r=0.6 было получено для n=50,
то выборочное значение статистики u было бы равно 4.75, и
гипотеза однозначно должна бы была быть отвергнута не только на уровне
значимости 5%, но и 1% (и даже более высоком, т.к. вероятность того, что стандартно распределенная случайная
величина примет значение большее 4.75 равна
0.000001).
3.10. Критерии согласия
Все
рассмотренные до сих пор критерии принято относить к группе так называемых параметрических
критериев. Применение этих критериев требует знания типа распределения
наблюдаемых случайных величин (нормальное, биномиальное, пуассоновское,
двумерное нормальное или какое-либо иное) и проверяемая гипотеза касается
параметров данных распределений. Прежде чем применять параметрические методы,
необходимо убедиться в том, что мы действительно имеем дело с распределением
требуемого типа.
Предположение о виде распределения
случайной величины – это статистическая гипотеза, которую можно проверить с
помощью экспериментальных данных. Критерии, позволяющие решать такого рода
задачи, называются критериями согласия – согласия выборочных данных некоторому
наперед заданному теоретическому распределению.
Пусть имеется выборка х1,
х2, ..., хп значений
случайной величины 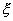 с неизвестной функцией распределения
F(x). Требуется проверить гипотезу
с неизвестной функцией распределения
F(x). Требуется проверить гипотезу 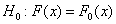 о
том, что случайная величина имеет некоторое заданное распределение F0(x) против альтернативной гипотезы
о
том, что случайная величина имеет некоторое заданное распределение F0(x) против альтернативной гипотезы 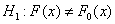 .
Распределение F0(x) может
быть либо задано полностью (простая нулевая гипотеза), либо с точностью до
параметров (сложная нулевая гипотеза). Во втором случае фактически проверяется
принадлежность распределения к заданному типу, например, проверяется гипотеза о
нормальности. Часто это делается с целью обоснования применения для обработки
полученных данных методов, требующих принадлежности распределения к заданному
типу (например, при применении t-критерия предполагается, что
выборка извлечена из нормальной генеральной совокупности). Следует однако
помнить, что неотвержение гипотезы
.
Распределение F0(x) может
быть либо задано полностью (простая нулевая гипотеза), либо с точностью до
параметров (сложная нулевая гипотеза). Во втором случае фактически проверяется
принадлежность распределения к заданному типу, например, проверяется гипотеза о
нормальности. Часто это делается с целью обоснования применения для обработки
полученных данных методов, требующих принадлежности распределения к заданному
типу (например, при применении t-критерия предполагается, что
выборка извлечена из нормальной генеральной совокупности). Следует однако
помнить, что неотвержение гипотезы 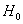 не
является убедительным доводом в пользу ее справедливости при неизвестной ошибке
второго рода, которая может быть довольно высокой при небольшом числе
наблюдений.
не
является убедительным доводом в пользу ее справедливости при неизвестной ошибке
второго рода, которая может быть довольно высокой при небольшом числе
наблюдений.
Для проверки гипотезы о принадлежности
распределения к заданному типу часто используется так называемый критерий
согласия 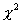 . Относительно распределения F(x) не делается никаких предположений, оно может быть
как непрерывным, так и дискретным. Статистика критерия
. Относительно распределения F(x) не делается никаких предположений, оно может быть
как непрерывным, так и дискретным. Статистика критерия 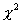 вычисляется
следующим образом. Область изменения значений выборки разбивается на k интервалов с таким расчетом, чтобы число
наблюдений ni (наблюденная частота)
в большинстве из интервалов i, i=1, …, k, было не менее 10. Для каждого из интервалов
вычисляется также вероятность pi попадания
в этот интервал случайной величины при условии выполнения гипотезы H0.
Статистика
вычисляется
следующим образом. Область изменения значений выборки разбивается на k интервалов с таким расчетом, чтобы число
наблюдений ni (наблюденная частота)
в большинстве из интервалов i, i=1, …, k, было не менее 10. Для каждого из интервалов
вычисляется также вероятность pi попадания
в этот интервал случайной величины при условии выполнения гипотезы H0.
Статистика 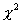 равна нормированной сумме квадратов
отклонений числа наблюдений ni от
гипотетической частоты npi
равна нормированной сумме квадратов
отклонений числа наблюдений ni от
гипотетической частоты npi
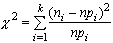
Для легкости запоминания эту формулу
можно рассматривать как сумму квадратов пуассоновских случайных величин ni, стандартизованных путем вычитания из
них гипотетических средних npi и
деления разности на их среднеквадратические отклонения (npi)1/2.
Если верна гипотеза H0
и при достаточно большом n (не менее 50)
распределение данной статистики хорошо приближается распределением 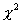 с
k-1-l степенями свободы, где l
- число параметров гипотетического распределения F0(x), оцененных по выборке (одна степень свободы
вычитается даже при полностью заданном F0(x),
поскольку наблюдаемые частоты связаны соотношением n1+n2+…+nk=n). Следовательно, критическое
множество уровня значимости
с
k-1-l степенями свободы, где l
- число параметров гипотетического распределения F0(x), оцененных по выборке (одна степень свободы
вычитается даже при полностью заданном F0(x),
поскольку наблюдаемые частоты связаны соотношением n1+n2+…+nk=n). Следовательно, критическое
множество уровня значимости  состоит из одного полуинтервала
состоит из одного полуинтервала 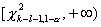 где
где
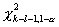 -
квантиль
-
квантиль 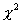 -распределения с числом степеней свободы k-l-1 порядка
-распределения с числом степеней свободы k-l-1 порядка 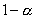 .
.
Необходимость в проверке простых
гипотез возникает относительно редко. Гораздо чаще F0(x) бывает известна с точностью до r параметров, 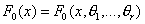 ,
где
,
где 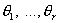 – неизвестные параметры. В этом
случае теоретические вероятности pi
не удается вычислить непосредственно, поэтому находим
– неизвестные параметры. В этом
случае теоретические вероятности pi
не удается вычислить непосредственно, поэтому находим 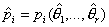 , i=1,…,k, где
, i=1,…,k, где 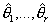 - оценки параметров
- оценки параметров 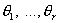 , определяемые
через наблюдаемые частоты n1,…,nk. Статистика критерия имеет вид
, определяемые
через наблюдаемые частоты n1,…,nk. Статистика критерия имеет вид
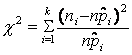
Если нулевая гипотеза H0 верна, статистика критерия 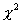 при
при 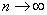 распределена
асимптотически как
распределена
асимптотически как 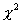 с числом степеней свободы k-r-1. Следовательно, критическое
множество уровня значимости
с числом степеней свободы k-r-1. Следовательно, критическое
множество уровня значимости  состоит из полуинтервала
состоит из полуинтервала 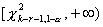 где
где
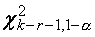 -
квантиль
-
квантиль 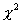 -распределения с числом степеней свободы k-r-1 порядка
-распределения с числом степеней свободы k-r-1 порядка 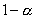 .
.
Часто оценки неизвестных параметров 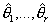 определяются не по наблюдаемым
частотам ni, а по всей выборке. Например, при
проверке нормальности ожидаемую частоту в i-ом
интервале, n
определяются не по наблюдаемым
частотам ni, а по всей выборке. Например, при
проверке нормальности ожидаемую частоту в i-ом
интервале, n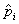 , находят, используя выборочное
среднее
, находят, используя выборочное
среднее 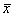 и выборочную дисперсию s2, определенные по всей выборке. В
этом случае статистика критерия
и выборочную дисперсию s2, определенные по всей выборке. В
этом случае статистика критерия 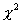 при справедливости H0 уже не имеет асимптотически
распределения
при справедливости H0 уже не имеет асимптотически
распределения 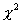 , ее распределение заключено между
, ее распределение заключено между 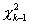 и
и
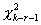 .
Различием между ними можно пренебречь при больших k. Но для малых k при определении критического
множества полезно убедиться, что выборочное значение статистики критерия
.
Различием между ними можно пренебречь при больших k. Но для малых k при определении критического
множества полезно убедиться, что выборочное значение статистики критерия 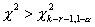 и
и
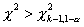 [3].
[3].
Для проверки соответствия
непрерывного распределения F(x) заданному F0(x) используются также одновыборочные
критерии Колмогорова и Смирнова. Статистика Колмогорова для проверки
гипотезы H0 против двусторонней альтернативы 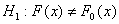 определяется как
максимум модуля отклонения эмпирической функции распределения
определяется как
максимум модуля отклонения эмпирической функции распределения 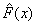 от
гипотетической F0(x)
от
гипотетической F0(x)
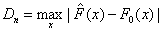
Статистика Смирнова, 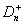 , для проверки гипотезы H0 против правосторонней альтернативы
, для проверки гипотезы H0 против правосторонней альтернативы 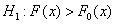 имеет
вид
имеет
вид
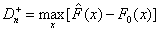
Для случая простой нулевой гипотезы
распределения статистик Dn и 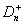 при справедливости
H0 не зависят от типа F0(x). Если верна нулевая гипотеза, предельным
распределением статистики
при справедливости
H0 не зависят от типа F0(x). Если верна нулевая гипотеза, предельным
распределением статистики 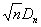 при
при 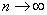 является распределение
Колмогорова, а Н.В. Смирнов получил точное и предельное распределение
статистики
является распределение
Колмогорова, а Н.В. Смирнов получил точное и предельное распределение
статистики 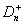 . Соответственно, критическое множество
уровня значимости
. Соответственно, критическое множество
уровня значимости  для проверки гипотезы H0
против двусторонней альтернативы H1 состоит из полуинтервала
для проверки гипотезы H0
против двусторонней альтернативы H1 состоит из полуинтервала 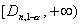 , и
против правосторонней альтернативы H1 -
, и
против правосторонней альтернативы H1 - 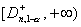 , где
, где 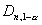 ,
, 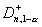 –
критические значения статистик Dn и
–
критические значения статистик Dn и 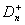 , соответственно, уровня
значимости
, соответственно, уровня
значимости  . При
. При 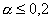
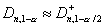 с
большой точностью (большей 0,00005). Поэтому критические значения статистики
с
большой точностью (большей 0,00005). Поэтому критические значения статистики 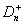 могут
быть заменены критическими значениями статистики Dn.
могут
быть заменены критическими значениями статистики Dn.
В случае сложной нулевой гипотезы,
когда F0(x) известна с
точностью до параметров, 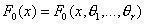 , где
, где 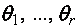 – неизвестные
параметры, статистика критерия для проверки гипотезы H0 против двусторонней альтернативы H1 имеет вид
– неизвестные
параметры, статистика критерия для проверки гипотезы H0 против двусторонней альтернативы H1 имеет вид
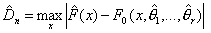
где 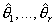 - оценки неизвестных параметров.
- оценки неизвестных параметров.
При условии, что нулевая гипотеза H0
верна, распределение статистики 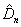 (и
(и 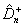 ) уже зависит от
конкретного вида распределения
) уже зависит от
конкретного вида распределения 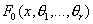 . Для некоторых типов распределений –
нормального, показательного, логистического – Лиллифорсом получены таблицы критических значений
статистики
. Для некоторых типов распределений –
нормального, показательного, логистического – Лиллифорсом получены таблицы критических значений
статистики 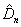 при условии, что гипотеза H0
верна [8, 9]. Соответственно, критическое множество уровня значимости
при условии, что гипотеза H0
верна [8, 9]. Соответственно, критическое множество уровня значимости  для
проверки гипотезы H0 против двусторонней альтернативы H1
состоит из одного полуинтервала
для
проверки гипотезы H0 против двусторонней альтернативы H1
состоит из одного полуинтервала 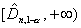 , где
, где 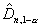 – критическое
значение статистики
– критическое
значение статистики 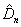 для заданных
для заданных  , n и F0(x).
, n и F0(x).
Статистика 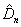 может
быть преобразована к виду, практически не зависящему от n.
Например, для нормального распределения Стефенсом
получено следующее выражение для модифицированной формы статистики Колмогорова
может
быть преобразована к виду, практически не зависящему от n.
Например, для нормального распределения Стефенсом
получено следующее выражение для модифицированной формы статистики Колмогорова 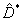 [5]:
[5]:
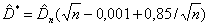
Это дает возможность проводить
проверку гипотезы практически при всех n, зная
значения 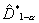 для небольшого набора значений
для небольшого набора значений  . В
частности, для
. В
частности, для 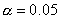 имеем
имеем 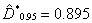 .
.
При проверке гипотезы о нормальности
распределения с неизвестными средним и дисперсией критерий Колмогорова-Смирнова
является более мощным, чем критерий 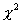 .
.
Заметим, что в
англоязычной литературе и в ППП статистики Dn и 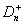 называют одновыборочными
статистиками Колмогорова-Смирнова, двусторонней и односторонней,
соответственно.
называют одновыборочными
статистиками Колмогорова-Смирнова, двусторонней и односторонней,
соответственно.
Среди других критериев согласия
отметим критерий Шапиро - Уилка для проверки
нормальности [6].
Если для конкретной выборки мы
отклоняем гипотезу о нормальности, и, следовательно, не имеем права
пользоваться методами, основанными на нормальности, то для получения
статистических выводов можно поступать разными способами. Например, если объем
выборки достаточно велик, можно предпочесть использовать параметрические
критерии как приближенные. Другой путь состоит в подборе замены переменной,
приводящей к нормальному распределению. Третий путь - применение непараметрических
критериев.
Пример. Пусть получена следующая выборка
50 значений случайной величины 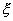 с неизвестным распределением:
с неизвестным распределением:
|
45
|
89
|
93
|
40
|
91
|
60
|
2
|
59
|
87
|
78
|
|
57
|
39
|
50
|
0
|
35
|
91
|
67
|
62
|
25
|
93
|
|
19
|
98
|
55
|
78
|
34
|
45
|
86
|
31
|
15
|
95
|
|
50
|
52
|
35
|
66
|
0
|
44
|
93
|
36
|
29
|
44
|
|
17
|
85
|
17
|
63
|
34
|
43
|
100
|
75
|
84
|
9
|
Проверим гипотезу о том, что эта
случайная величина имеет нормальное распределение. После разбиения области
изменения выборочных значений на 5 равных интервалов получаем следующие
наблюденные и гипотетические частоты:
|
Интервал
|
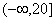
|
(20, 40]
|
(40, 60]
|
(60, 80]
|
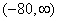
|
|
Наблюденная частота, nI
|
8
|
10
|
12
|
7
|
13
|
|
Гипотетическая
Частота, npi
|
6.1
|
9.7
|
13.4
|
11.6
|
9.2
|
Гипотетические частоты вычислялись
для нормального распределения 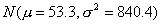 с параметрами, оцененными по выборке
- соответственно, число степеней свободы статистики критерия равно 5-1-2=2.
Выборочное значение статистики равно
с параметрами, оцененными по выборке
- соответственно, число степеней свободы статистики критерия равно 5-1-2=2.
Выборочное значение статистики равно 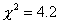 , что не выходит за
критический 5%-ный предел, равный
, что не выходит за
критический 5%-ный предел, равный 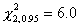 . Следовательно, у нас
нет оснований отвергнуть гипотезу о нормальности.
. Следовательно, у нас
нет оснований отвергнуть гипотезу о нормальности.
В действительности, выборка была
получена с помощью датчика случайных чисел, равномерно распределенных на
отрезке [0, 100]. Т.е. мы видим, что при данном числе наблюдений (в общем-то,
конечно, небольшом для проверки гипотезы о типе распределения) критерий 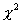 не
обнаруживает отклонения от нормальности в направлении равномерности.
не
обнаруживает отклонения от нормальности в направлении равномерности.
Величина статистики одновыборочного критерия Колмогорова - Смирнова равна D=0.11,
что также не выходит за 5%-ный предел этого критерия в предположении, что
гипотетические средние равны выборочным. Однако в случае неизвестных параметров
гипотетического нормального распределения лучше пользоваться модификацией
критерия Колмогорова - Смирнова, предложенной Cтефенсом (Лиллифорсом).
Но в этом случае значение 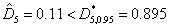 , т.е. нет оснований отвергнуть гипотезу и
по этому критерию.
, т.е. нет оснований отвергнуть гипотезу и
по этому критерию.
Пример. Расчеты, аналогичные предыдущим,
проведенные для выборки объема 150 значений случайной величины, равномерно
распределенной на отрезке [0, 100], дали значение 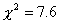 , что позволило
отвергнуть гипотезу о нормальности на уровне значимости 5%. По критерию
Колмогорова - Смирнова гипотеза отвергалась лишь на уровне 10%, а по критерию Лиллифорса - на уровне 1%, что показывает неправомочность
применения критерия Колмогорова - Смирнова в данной ситуации.
, что позволило
отвергнуть гипотезу о нормальности на уровне значимости 5%. По критерию
Колмогорова - Смирнова гипотеза отвергалась лишь на уровне 10%, а по критерию Лиллифорса - на уровне 1%, что показывает неправомочность
применения критерия Колмогорова - Смирнова в данной ситуации.
Пример. Расчеты статистик критериев
согласия для данных таблицы 1, содержащей 50 выборочных значений длины лепестка
ириса разноцветного, приводят к значению статистики 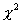 равному
2.1, и значению статистики
равному
2.1, и значению статистики 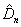 , равному 0.117. В этом случае гипотеза о
нормальности не отвергается ни критерием
, равному 0.117. В этом случае гипотеза о
нормальности не отвергается ни критерием 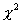 , ни критерием
Колмогорова - Смирнова - Лиллифорса.
, ни критерием
Колмогорова - Смирнова - Лиллифорса.
Пример. В некоторых классических
экспериментах с селекцией гороха Мендель наблюдал частоты различных видов
семян, получаемых при скрещивании растений с круглыми желтыми семенами и
растений с морщинистыми зелеными семенами. Они приводятся ниже вместе с
теоретическими вероятностями, вычисленными в соответствии с теорией
наследственности Менделя.
|
Семена
|
Наблюденная численность
|
Ожидаемая численность
|
|
Круглые и желтые
|
315
|
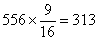
|
|
Морщинистые и желтые
|
101
|
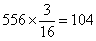
|
|
Круглые и зеленые
|
108
|
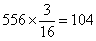
|
|
Морщинистые и зеленые
|
32
|
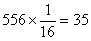
|
|
Всего
|
556
|
556
|
В этом случае теоретическое
распределение дискретно и известно полностью. Для проверки согласия
экспериментальных данных теоретическому распределению используем критерий 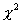 для
простой гипотезы. Значение статистики, вычисленное по выборке равно
для
простой гипотезы. Значение статистики, вычисленное по выборке равно 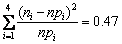 ,
что меньше 5%-ного критического значения
,
что меньше 5%-ного критического значения 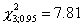 . Следовательно, теория
наследственности Менделя не противоречит полученным экспериментальным данным.
. Следовательно, теория
наследственности Менделя не противоречит полученным экспериментальным данным.
Наряду с количественными
статистическими критериями для определения типа распределения по выборочным
данным используются графические методы.
Простейший способ - построение по
имеющейся выборке гистограммы относительных частот и на том же графике и в том
же масштабе, - кривой плотности нормального распределения с выборочным средним
и выборочной дисперсией в качестве параметров. Значительные отклонения от
нормальности (сильная асимметрия, бимодальность)
легко обнаруживаются на графике.
Пример. Применим этот прием к
рассмотренной выше модельной выборке объема n=50, извлеченной из равномерного
распределения. На рис. 7 приведена гистограмма и кривая нормальной плотности.
Можно сказать, что визуально отклонение от нормальности в пользу равномерности
заметно (хотя, как мы видели, статистически значимо при таком числе наблюдений
оно не подтверждается).
С точки зрения визуального
обнаружения отклонений от нормальности сравнение эмпирической и гипотетической
функций распределения гораздо менее наглядно, чем сравнение гистограммы с
графиком плотности. Однако обычно сравнивают на сами функции распределения, а
обратные нормальные преобразования от них, так называемые пробит-графики.
Пробит-график от теоретической нормальной функции
распределения представляет собой прямую, а пробит-график
эмпирической функции распределения тем ближе к прямой, чем ближе она к
нормальной. Этот прием позволяет на первом этапе анализа данных выявить их
особенности, выдвинуть гипотезы о характере распределения, решить вопрос о
целесообразности замены переменной.
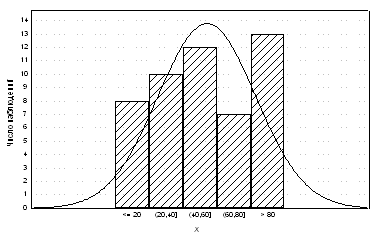
Рис. 7.
Пример сравнения гистограммы и кривой нормальной плотности.
3.11. Непараметрические критерии
В большинстве случаев надежная
априорная информация о типе распределения отсутствует, а имеющиеся выборочные
данные слишком малочисленны для определения типа распределения. В этих
ситуациях применяются так называемые непараметрические критерии,
характеризующиеся тем, что в качестве их статистик используются такие функции
от наблюдений, распределение которых не зависит от вида распределения
наблюдаемых случайных величин.
Часто статистики непараметрических
критериев основаны не непосредственно на численных значениях наблюдений выборки
х1, х2, ..., хп,
а на их рангах, т.е. на порядковых номерах R(x1),
R(x2), …, R(xп)
наблюдений при их упорядочении по возрастанию (в их вариационном ряду). Ранги
наблюдений, будучи функциями выборочных значений, являются случайными
величинами с возможными значениями 1, 2, …, n.
Оказалось, что набор рангов R(x1), R(x2),
…, R(xп) cодержит
значительную долю информации о распределении наблюдаемой случайной величины,
что обеспечивает этим методам высокую эффективность.
Если статистика рангового критерия, g(R1, R2,…,Rn), – дискретная случайная величина,
то для заданного уровня значимости  может не
существовать значения квантили распределения статистики критерия при
справедливости нулевой гипотезы порядка
может не
существовать значения квантили распределения статистики критерия при
справедливости нулевой гипотезы порядка  . Поэтому для
определения критического множества используется верхнее критическое значение
статистики критерия
. Поэтому для
определения критического множества используется верхнее критическое значение
статистики критерия 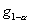 , равное наименьшему значению g, такому, что
, равное наименьшему значению g, такому, что 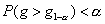 , и
нижнее критическое значение
, и
нижнее критическое значение 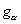 , равное наибольшему значению g, такому, что
, равное наибольшему значению g, такому, что 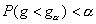 . Значения
. Значения 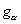 и
и
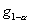 находятся по таблицам. Для всех рассматриваемых
критериев существуют таблицы критических значений статистики, например, в [1,
2, 7].
находятся по таблицам. Для всех рассматриваемых
критериев существуют таблицы критических значений статистики, например, в [1,
2, 7].
Важной особенностью ранговых критериев является их применимость
и в тех случаях, когда наблюдения не являются количественными, но допускают
упорядочение, что часто имеет место в исследованиях по биологии, медицине,
психологии и социологии. Рассмотрим некоторые непараметрические критерии.
3.11.1. Одновыборочные
критерии
Ряд одновыборочных
критериев предназначен для проверки гипотезы о равенстве медианы заданному
значению. Пусть имеется выборка х1, х2,
..., хп значений случайной величины 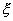 с
неизвестной функцией распределения F(x,
M) и неизвестной медианой M. Требуется проверить гипотезу
с
неизвестной функцией распределения F(x,
M) и неизвестной медианой M. Требуется проверить гипотезу 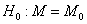 о
равенстве медианы M заданному числу M0.
о
равенстве медианы M заданному числу M0.
Для решения этой задачи можно
воспользоваться критерием знаков. Возьмем в качестве статистики
критерия число 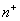 положительных разностей среди n разностей хi - M0, i=1,…, n. Если верна нулевая гипотеза H0, то
P(xi>M0)=P(xi<M0)=1/2 и,
следовательно, статистика критерия
положительных разностей среди n разностей хi - M0, i=1,…, n. Если верна нулевая гипотеза H0, то
P(xi>M0)=P(xi<M0)=1/2 и,
следовательно, статистика критерия 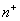 – дискретная
случайная величина, распределенная по биномиальному закону с параметрами n и p=1/2.
– дискретная
случайная величина, распределенная по биномиальному закону с параметрами n и p=1/2.
Критическая область уровня
значимости  для проверки гипотезы
для проверки гипотезы 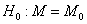 против
двусторонней альтернативы
против
двусторонней альтернативы 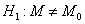 будет состоять из двух интервалов
будет состоять из двух интервалов 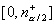 и
и
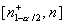 ,
причем
,
причем 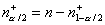 , так как распределение статистики
критерия
, так как распределение статистики
критерия 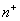 при H0 симметрично относительно своего
среднего n/2,
а
при H0 симметрично относительно своего
среднего n/2,
а 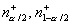 - нижнее и верхнее критические
значения статистики
- нижнее и верхнее критические
значения статистики 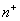 , соответственно. Критическая область
против правосторонней альтернативы
, соответственно. Критическая область
против правосторонней альтернативы 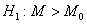 состоит из одного
интервала
состоит из одного
интервала 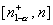 и против левосторонней альтернативы
и против левосторонней альтернативы 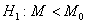 -
также из одного интервала
-
также из одного интервала 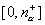 .
.
При малых n
критические значения можно вычислить точно с помощью непосредственного перебора
равновозможных 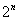 последовательностей с
последовательностей с 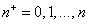 . При
. При 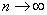 случайная
величина
случайная
величина 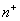 распределена асимптотически
нормально,
распределена асимптотически
нормально, 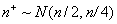 , и для нахождения критических значений
можно воспользоваться нормальным приближением.
, и для нахождения критических значений
можно воспользоваться нормальным приближением.
Критерий знаков обладает
недостаточной чувствительностью к различению нулевой и альтернативной гипотез
(его асимптотическая эффективность по отношению к одновыборочному
t-критерию равна 0,637), но из-за простоты и наглядности часто
используется для предварительного анализа данных.
Большей мощностью обладает критерий
знаковых рангов (асимптотическая эффективность по отношению к одновыборочному t-критерию равна 0,955). Статистика
знаковых рангов Вилкоксона равна сумме рангов
положительных разностей
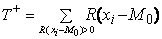
где 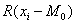 ранг разности
ранг разности 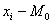 и
суммирование рангов ведется по положительным разностям.
и
суммирование рангов ведется по положительным разностям.
Если нулевая гипотеза H0 верна, вероятность каждого из
возможных 2n исходов для набора рангов положительных разностей равна
(1/2)n, что и определяет распределение статистики критерия для
заданного n, симметричного относительно среднего n(n+1)/4, откуда следует, что 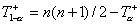 . где
. где 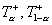 – верхнее и нижнее
критические значения статистики критерия при заданных
– верхнее и нижнее
критические значения статистики критерия при заданных  и n, соответственно. Критическая
область уровня значимости
и n, соответственно. Критическая
область уровня значимости  для проверки гипотезы
для проверки гипотезы 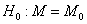 против
двусторонней альтернативы
против
двусторонней альтернативы 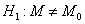 будет состоять из двух интервалов
будет состоять из двух интервалов 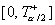 и
и
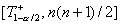 .
Критическая область против правосторонней альтернативы
.
Критическая область против правосторонней альтернативы 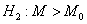 - из
одного интервала
- из
одного интервала 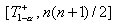 и против левосторонней альтернативы
и против левосторонней альтернативы 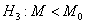 -
также из одного интервала
-
также из одного интервала 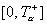 .
.
Если верна 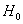 , то при
, то при 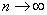 распределение
статистики критерия стремится к нормальному,
распределение
статистики критерия стремится к нормальному, 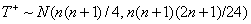 . При n>25 этим приближением можно воспользоваться для
определения критических значений статистики.
. При n>25 этим приближением можно воспользоваться для
определения критических значений статистики.
3.11.2. Проверка гипотезы об
отсутствии сдвига
Пусть имеются выборки х1,
х2, ..., хп и y1,
y2, ..., ym значений
случайных величин 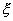 и
и 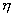 с неизвестными
функциями распределения F(x) и G(x). Известно однако, что F(x) и G(x)
имеют одинаковую форму и различаются лишь сдвигом, т.е.
с неизвестными
функциями распределения F(x) и G(x). Известно однако, что F(x) и G(x)
имеют одинаковую форму и различаются лишь сдвигом, т.е. 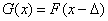 . Требуется
проверить гипотезу
. Требуется
проверить гипотезу 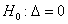 об отсутствии сдвига между
распределениями случайных величин
об отсутствии сдвига между
распределениями случайных величин 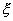 и
и 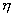 .
.
Случай
независимых выборок
Пусть x1,…,xn и y1,…,ym – независимые выборки из
непрерывных распределений F(x) и G(x), соответственно, причем 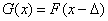 . Для решения
задачи об отсутствии сдвига между F(x) и G(x) можно применить критерий Вилкоксона или критерий Манна - Уитни.
Пусть
. Для решения
задачи об отсутствии сдвига между F(x) и G(x) можно применить критерий Вилкоксона или критерий Манна - Уитни.
Пусть 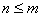 - в противном случае выборки поменяем местами.
Упорядочим n+m наблюдений по возрастанию и обозначим через Ri ранг i-ого наблюдения в объединенном ряду,
i=1,…,n+m. Если есть совпадающие значения
внутри какой-либо из выборок, то ранги их можно взять в произвольном порядке.
Если же совпадают значения, принадлежащие разным выборкам, то их ранги
заменяются средним арифметическим рангов, которые бы получились, если бы
наблюдения различались.
- в противном случае выборки поменяем местами.
Упорядочим n+m наблюдений по возрастанию и обозначим через Ri ранг i-ого наблюдения в объединенном ряду,
i=1,…,n+m. Если есть совпадающие значения
внутри какой-либо из выборок, то ранги их можно взять в произвольном порядке.
Если же совпадают значения, принадлежащие разным выборкам, то их ранги
заменяются средним арифметическим рангов, которые бы получились, если бы
наблюдения различались.
В качестве статистики Манна-Уитни U используется общее число случаев
(инверсий) в упорядоченной по возрастанию последовательности из x и y, в которых x появляется позднее некоторого y:
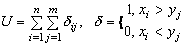
Если xi=yj, к значению U прибавляется 1/2. Статистика U – дискретная случайная величина,
принимающая значения от 0 до nm.
Если нулевая гипотеза H0 верна, 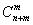 последовательностей
из x и y являются равновероятными, что и определяет распределение статистики U, симметричное относительно своего
среднего nm/2. Критическая область уровня значимости
последовательностей
из x и y являются равновероятными, что и определяет распределение статистики U, симметричное относительно своего
среднего nm/2. Критическая область уровня значимости  для проверки
гипотезы
для проверки
гипотезы 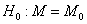 против двусторонней альтернативы
против двусторонней альтернативы 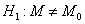 будет
состоять из двух интервалов
будет
состоять из двух интервалов 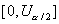 и
и 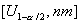 , где
, где 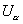 и
и 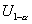 - нижнее и верхнее критические
значения статистики критерия U, связанные соотношением
- нижнее и верхнее критические
значения статистики критерия U, связанные соотношением 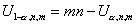 . Критическая область против
правосторонней альтернативы
. Критическая область против
правосторонней альтернативы 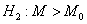 - из одного интервала
- из одного интервала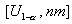 и
против левосторонней альтернативы
и
против левосторонней альтернативы 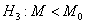 - из одного интервала
- из одного интервала 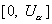 .
.
При малых n и m значение 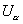 определяется непосредственным
подсчетом последовательностей с наименьшим количеством инверсий. При больших n и m распределение U можно аппроксимировать нормальным
распределением. Если нулевая гипотеза H0 верна, то при
определяется непосредственным
подсчетом последовательностей с наименьшим количеством инверсий. При больших n и m распределение U можно аппроксимировать нормальным
распределением. Если нулевая гипотеза H0 верна, то при 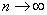 ,
, 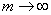
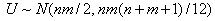 , и для вычисления критических
значений можно воспользоваться нормальным приближением.
, и для вычисления критических
значений можно воспользоваться нормальным приближением.
Статистику критерия U можно также вычислить по формуле
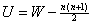
где 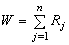 , сумма рангов наблюдений xj, j=1, …, n, есть статистика критерия Вилкоксона. Следовательно критерии, основанные на
статистиках U и W эквивалентны.
, сумма рангов наблюдений xj, j=1, …, n, есть статистика критерия Вилкоксона. Следовательно критерии, основанные на
статистиках U и W эквивалентны.
Пример. Пусть получены выборки значений
двух случайных величин 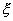 и
и 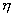 объема n=4
и m=5:
объема n=4
и m=5:
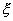 : 174 175
183 174
: 174 175
183 174
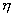 : 187 185
185 179 181
: 187 185
185 179 181
Составим из них общий вариационный
ряд (т.е. расположим в порядке возрастания), сохранив информацию о
принадлежности к выборке:
|
Ранг
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
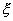
|
174
|
174
|
175
|
|
|
183
|
|
|
|
|
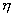
|
|
|
|
179
|
181
|
|
185
|
185
|
187
|
Сумма рангов выборки значений
случайной величины 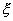 равна W=1+2+3+6=12. Это значение не выходит
за двусторонние критические пределы W0.025=11 и W0.975=34 уровня значимости 5%. Выборочное
значение статистики U=2 и соответствующее ему p=0.032 меньше 0.05 и, следовательно,
у нас нет оснований отвергнуть нулевую гипотезу о том, что сдвиг между
распределениями F(x) и G(x) отсутствует.
равна W=1+2+3+6=12. Это значение не выходит
за двусторонние критические пределы W0.025=11 и W0.975=34 уровня значимости 5%. Выборочное
значение статистики U=2 и соответствующее ему p=0.032 меньше 0.05 и, следовательно,
у нас нет оснований отвергнуть нулевую гипотезу о том, что сдвиг между
распределениями F(x) и G(x) отсутствует.
Заметим, что приведенные данные были
получены с помощью датчика нормально распределенных случайных чисел 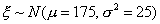 и
и
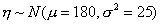 .
Приведенные выше значения могли бы быть, например, значениями роста четырех
случайно выбранных французов и пяти случайно выбранных норвежцев (средний рост
взрослых мужчин Франции и Норвегии равен 175 и 180 см, соответственно).
Т.е. в действительности сдвиг
.
Приведенные выше значения могли бы быть, например, значениями роста четырех
случайно выбранных французов и пяти случайно выбранных норвежцев (средний рост
взрослых мужчин Франции и Норвегии равен 175 и 180 см, соответственно).
Т.е. в действительности сдвиг  между распределениями отличен от
нуля (он равен
между распределениями отличен от
нуля (он равен  =175-180=-5) и гипотеза
=175-180=-5) и гипотеза 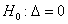 неверна,
но критерии Вилкоксона и Манна - Уитни не обнаружили
различия между распределениями F(x) и G(x). Если применить к приведенным данным t-критерий
Стьюдента для сравнения математических ожиданий двух нормально распределенных
случайных величин с неизвестными дисперсиями, то получим выборочное значение t=-2.72
для статистики критерия. Поскольку это значение выходит за 5%-ные критические
пределы t7,0.025=-2.36 и t7,0.975=2.36 t-распределения
с 4+5-2=7 степенями свободы, то гипотеза о равенстве математических ожиданий
должна быть отвергнута. Это типичная ситуация - непараметрические критерии
обладают меньшей мощностью по сравнению с аналогичными параметрическими
критериями, использующими дополнительную информацию о наблюдаемых случайных
величинах. Поэтому, если имеется достоверная дополнительная информация, то
предпочтительнее использовать критерий, учитывающий эту информацию.
неверна,
но критерии Вилкоксона и Манна - Уитни не обнаружили
различия между распределениями F(x) и G(x). Если применить к приведенным данным t-критерий
Стьюдента для сравнения математических ожиданий двух нормально распределенных
случайных величин с неизвестными дисперсиями, то получим выборочное значение t=-2.72
для статистики критерия. Поскольку это значение выходит за 5%-ные критические
пределы t7,0.025=-2.36 и t7,0.975=2.36 t-распределения
с 4+5-2=7 степенями свободы, то гипотеза о равенстве математических ожиданий
должна быть отвергнута. Это типичная ситуация - непараметрические критерии
обладают меньшей мощностью по сравнению с аналогичными параметрическими
критериями, использующими дополнительную информацию о наблюдаемых случайных
величинах. Поэтому, если имеется достоверная дополнительная информация, то
предпочтительнее использовать критерий, учитывающий эту информацию.
Гипотезу об отсутствии сдвига можно
проверить также с помощью критерия Ван-дер-Вардена.
Обозначим N=n+m. Статистика
критерия имеет вид
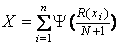
где R(xi) - ранг наблюдения xi,
а 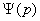 -
p-квантиль стандартного нормального распределения.
-
p-квантиль стандартного нормального распределения.
Если нулевая гипотеза H0
верна, то 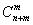 последовательностей длиной N
из xi и yi являются
равновероятными. При малых n и m критические значения можно вычислить точно с
помощью непосредственного перебора равновозможных последовательностей из x и y. Верхнее,
последовательностей длиной N
из xi и yi являются
равновероятными. При малых n и m критические значения можно вычислить точно с
помощью непосредственного перебора равновозможных последовательностей из x и y. Верхнее, 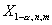 , и нижнее,
, и нижнее, 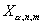 , критические значения,
соответствующие уровню значимости
, критические значения,
соответствующие уровню значимости 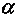 , при заданных n и m связаны соотношением
, при заданных n и m связаны соотношением 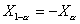 . Критическая область уровня
значимости
. Критическая область уровня
значимости  для проверки гипотезы
для проверки гипотезы 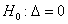 против
двусторонней альтернативы
против
двусторонней альтернативы 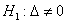 будет состоять из двух бесконечных
полуинтервалов
будет состоять из двух бесконечных
полуинтервалов 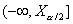 и
и 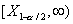 . Критическая область
против правосторонней альтернативы
. Критическая область
против правосторонней альтернативы 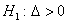 - из одного
полуинтервала
- из одного
полуинтервала 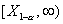 и против левосторонней альтернативы
и против левосторонней альтернативы 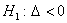 -
также из одного полуинтервала
-
также из одного полуинтервала 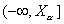 . При
. При 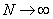 , независимо от
поведения n и m
по отдельности, статистика X распределена асимптотически нормально,
, независимо от
поведения n и m
по отдельности, статистика X распределена асимптотически нормально, 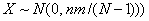 .
.
Критерий Ван-дер-Вардена
является наиболее мощным непараметрическим критерием для решения задачи двух
выборок, если функции распределений F(x)
и G(x) отличаются лишь параметром
сдвига. Если обе выборки извлечены из нормальных совокупностей, то при
постоянном n и 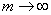 критерий
Ван-дер-Вардена имеет такую же мощность, как и двухвыборочный t-критерий.
критерий
Ван-дер-Вардена имеет такую же мощность, как и двухвыборочный t-критерий.
Случай
связанных выборок
Пусть x1,…, xn и y1,…, yn – связанные выборки из непрерывных
распределений F(x) и G(x), соответственно, причем 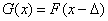 . Например,
каждая пара наблюдений (xi, yi), i=1,…, n, принадлежит одному объекту, либо (xi, yi) попарно связаны тем, что условия
проведения наблюдений менялись от опыта к опыту, но для каждой пары (xi, yi) оставались постоянными, что в
практике биологического эксперимента встречается очень часто.
. Например,
каждая пара наблюдений (xi, yi), i=1,…, n, принадлежит одному объекту, либо (xi, yi) попарно связаны тем, что условия
проведения наблюдений менялись от опыта к опыту, но для каждой пары (xi, yi) оставались постоянными, что в
практике биологического эксперимента встречается очень часто.
Обозначим
через zi=xi - yi. Тогда задача об отсутствии сдвига
между F(x) и G(x) сводится к одновыборочной задаче,
рассмотренной в 3.11.1. И для проверки гипотезы H0 можно применить критерий знаков или
критерий знаковых рангов.
Асимптотическая относительная
эффективность критерия знаков для связанных выборок по отношению к двухвыборочному t-критерию для связанных выборок
равна 0.637, а критерия знаковых рангов Вилкоксона –
0.955.
3.11.3. Критерии однородности
Критерии Манна – Уитни (Вилкоксона) и Ван-дер-Вардена
позволяют обнаруживать лишь различия в центральных тенденциях распределений
двух случайных величин. Если важно обнаружить любые расхождения в форме
распределений, то пользуются критериями однородности, например, двухвыборочным критерием Смирнова.
С помощью этого критерия проверяется гипотеза 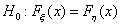 о том, что функции
распределения
о том, что функции
распределения 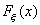 и
и 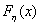 случайных величин
случайных величин 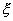 и
и
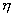 идентичны
против альтернативной гипотезы
идентичны
против альтернативной гипотезы 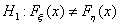 о том, что они различны.
о том, что они различны.
Статистика критерия Смирнова Dm,n определяется как максимум модуля
разности между эмпирической функцией 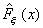 , построенной по выборке
х1, х2, ..., хп,
и эмпирической функцией
, построенной по выборке
х1, х2, ..., хп,
и эмпирической функцией 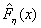 , построенной по выборке y1,
y2, ..., ym
, построенной по выборке y1,
y2, ..., ym
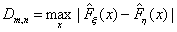
При справедливости гипотезы H0 статистика 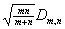 имеет
асимптотическое (при
имеет
асимптотическое (при 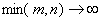 так, что отношение m/n остается постоянным) распределение
Колмогорова. Критическая область уровня значимости
так, что отношение m/n остается постоянным) распределение
Колмогорова. Критическая область уровня значимости  для
проверки гипотезы H0 против двусторонней альтернативы H1 будет состоять из одного
полуинтервала
для
проверки гипотезы H0 против двусторонней альтернативы H1 будет состоять из одного
полуинтервала 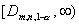 , где
, где 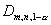 - квантиль
распределения статистики
- квантиль
распределения статистики 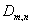 при H0 порядка
при H0 порядка 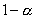 .
.
Заметим, что в англоязычной
литературе и в ППП критерий однородности двух выборок Смирнова называют двухвыборочным критерием
Колмогорова-Смирнова.
3.11.4. Проверка гипотезы о
независимости
Пусть имеется двумерная выборка (x1,
y1), (x2, y2), …, (xn, yn)
из неизвестного двумерного распределения. Причем наблюдаемые признаки могут
быть как количественными, так и порядковыми. Найдем ранги, R(xi) и R(yi),
в последовательностях x1, x2, …, xn и y1, y2, …, yn, упорядоченных по отдельности.
Мерой зависимости двух случайных величин, каждая из которых может быть как
количественной, так и порядковой, является коэффициент ранговой
корреляции Спирмена, определяемый формулой
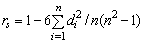
где di= R(xi)-R(yi).
Как и обычный коэффициент корреляции, коэффициент ранговой корреляции rs принимает значения 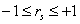 , причем rs=+1,
когда R(xi)=R(yi), i=1, …, n,
и rs=-1, когда последовательности рангов
полностью противоположны, R(xi)=(n+1)-R(yi), i=1, …, n.
Коэффициент rs используется для
проверки гипотезы о независимости признаков. Нулевая гипотеза формулируется как
, причем rs=+1,
когда R(xi)=R(yi), i=1, …, n,
и rs=-1, когда последовательности рангов
полностью противоположны, R(xi)=(n+1)-R(yi), i=1, …, n.
Коэффициент rs используется для
проверки гипотезы о независимости признаков. Нулевая гипотеза формулируется как
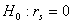 .
Чаще всего H0 проверяется против альтернативы
.
Чаще всего H0 проверяется против альтернативы 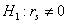 .
Статистикой критерия является rs.
Если нулевая гипотеза H0 верна, то распределение rs симметрично относительно 0 с Mrs=0
и Drs=1/(n-1). Следовательно, множество принятия
нулевой гипотезы имеет вид
.
Статистикой критерия является rs.
Если нулевая гипотеза H0 верна, то распределение rs симметрично относительно 0 с Mrs=0
и Drs=1/(n-1). Следовательно, множество принятия
нулевой гипотезы имеет вид 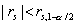 , где
, где 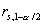 – верхнее
критическое значение статистики критерия rs,
соответствующее уровню значимости
– верхнее
критическое значение статистики критерия rs,
соответствующее уровню значимости  при заданном n.
при заданном n.
Если верна нулевая гипотеза,
случайная величина 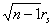 при
при 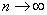 распределена
асимптотически нормально с параметрами (0, 1). При
распределена
асимптотически нормально с параметрами (0, 1). При 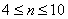 критические
значения статистики критерия находят по таблицам точного распределения rs при H0, а при n>10 пользуются нормальной аппроксимацией.
критические
значения статистики критерия находят по таблицам точного распределения rs при H0, а при n>10 пользуются нормальной аппроксимацией.
Асимптотическая
относительная эффективность критерия, основанного на rs,
по отношению к критерию, основанному на выборочном коэффициенте корреляции,
равна 0.912.
ЛИТЕРАТУРА
1. Благовещенский Ю.Н., Самсонова В.П., Дмитриев Е.А.
Непараметрические методы в почвенных исследованиях. М.: Наука, 1987.
2. Большев Л.Н., Смирнов Н.В. Таблицы
математической статистики. М.: Наука, 1983.
3. Кендалл М.Дж., Стьюарт
А. Статистические выводы и связи. М.: Наука, 1973
4. Компьютерная биометрика. М.: Изд-во МГУ, 1990
5. Тюрин Ю.Н. Непараметрические методы статистики. М.:
Знание, 1978.
6. Хан Г., Шапиро С. Статистические модели в инженерных
задачах. М.: Cтатистика, 1980.
7. Холлендер М., Вульф Д. Непараметрические
методы статистики. М.: Финансы и статистика, 1983.
8.
Lilliefors H.W. The Kolmogorov-Smirnov Test for Normality with Mean and
Variance Unknown. J. Amer. Stat. Assn. v.62: 399-402.
9.
Sokal R.R., Rohlf F.J. Biometry. The Principles and Practice of
Statistics in Biological Research. N-Y, 1995.

