МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
им. М.В. ЛОМОНОСОВА
БИОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ
В.Д. Мятлев, Л.А. Панченко, А. Т.
Терехин
ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Пособие по курсу
"Математические методы в
биологии"
МОСКВА
МАКС Пресс
2002
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. СЛУЧАЙНАЯ
ВЫБОРКА И ЕЕ ОПИСАНИЕ
1.1. Понятие
случайной выборки
1.2.
Характеристики случайной выборки
2.
СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
2.1. Логика
статистического оценивания
2.2.
Доверительные интервалы
2.2.1. Доверительный интервал для
математического ожидания нормально распределенной случайной величины с
известной дисперсией
2.2.2. Доверительный интервал для
математического ожидания нормально распределенной случайной величины с неизвестной
дисперсией
2.2.3. Доверительный интервал для неизвестной дисперсии нормально
распределенной случайной величины (при неизвестном математическом ожидании)
2.2.4. Доверительный интервал для неизвестного параметра p биномиального распределения
2.2.5. Доверительный интервал для неизвестного параметра l пуассоновского распределения
2.2.6. Приближенный доверительный интервал
для неизвестного коэффициента корреляции двумерного нормального распределения
3. ПРОВЕРКА СТАТИСТИЧЕСКИХ
ГИПОТЕЗ
3.1. Логика проверки статистических
гипотез
3.2. Проверка гипотезы о равенстве заданному
числу математического ожидания нормально распределенной случайной величины с
известной дисперсией
3.3. Проверка гипотезы о равенстве
заданному числу математического ожидания нормально распределенной случайной
величины
с неизвестной дисперсией (одновыборочный t-критерий)
3.4. Проверка гипотезы о равенстве
заданному числу дисперсии нормально распределенной случайной величины (одновыборочный
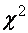 -критерий)
-критерий)
3.5. Проверка гипотезы о равенстве математических ожиданий двух
независимых нормально распределенных случайных величин (двухвыборочный t-критерий)
3.6. Проверка гипотезы о равенстве дисперсий двух независимых нормально
распределенных случайных величин (двухвыборочный F-критерий)
3.7. Приближенный критерий для проверки
гипотезы о равенстве параметров двух независимых биномиальных случайных величин
(критерий для сравнения двух вероятностей)
3.8. Приближенный критерий для проверки гипотезы о равенстве параметров
двух независимых пуассоновских случайных величин
3.9. Приближенный критерий для проверки
гипотезы о равенстве нулю коэффициента корреляции между компонентами двумерной
нормально распределенной случайной величины
3.10.. Критерии согласия
3.11. Непараметрические критерии
3.11.1. Одновыборочные критерии
3.11.2. Проверка гипотезы об
отсутствии сдвига
3.11.3.
Критерии однородности
3.11.4. Проверка гипотезы о независимости
ЛИТЕРАТУРА
ВВЕДЕНИЕ

Задача математической
статистики, в строгом понимании этого термина, состоит в разработке и
применении методов описания реальных явлений вероятностными моделями, исходя из
данных, полученных в результате наблюдений за этими явлениями.
В более широком смысле математическая
статистика понимается как совокупность методов планирования экспериментов и
обработки данных, полученных в результате экспериментов, причем эти методы
могут не основываться на вероятностных моделях. При таком широком понимании
вместо термина «математическая статистика» часто используют термин «анализ
данных».
Исторически вначале сформировались методы
обработки данных, не связанные тесно с теорией вероятности, так называемая
дескриптивная, описательная статистика. С начала этого века
начали интенсивно развиваться методы анализа данных, основанные на
вероятностных моделях, - это, прежде всего, методы статистического
оценивания и статистической проверки гипотез, о которых
будет идти речь в данной книге.
Бурное развитие вычислительной техники
вызвало к жизни ряд новых методов анализа. Некоторые из этих методов
разработаны на основе подходов, отличных от теоретико-вероятностного
(геометрические, оптимизационные и др.). Вероятностное их обоснование либо
отсутствует, либо недостаточно, что затрудняет количественную оценку степени
достоверности выводов и исследование аналитическими средствами классической
математической статистики. Однако в последние годы, также в связи с быстрым
ростом производительности вычислительных машин, начали получать распространение
процедуры так называемого случайного моделирования (пермутационные
методы, бут-стрэп), позволяющие оценить статистические свойства получаемых
решений без аналитических методов.
Начнем рассмотрение методов
математической статистики с ее исходного понятия - понятия случайной выборки.
1. СЛУЧАЙНАЯ
ВЫБОРКА И ЕЕ ОПИСАНИЕ
1.1. Понятие
случайной выборки
Понятие случайной выборки тесно связано с
понятием случайного испытания и случайной величины, о которых шла
речь в предыдущей главе. Случайная выборка представляет собой
совокупность наблюдений х1,х2,...,xn
случайной величины 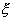 , полученных в п независимых случайных испытаниях.
Число полученных наблюдений п называется объемом выборки.
Образно можно представить процесс получения случайной выборки как извлечение
наудачу значений из гипотетической бесконечной генеральной
совокупности, где разные значения содержатся в пропорциях,
соответствующих распределению случайной величины, и тщательно перемешаны между
собой. Случайная величина может быть не только одномерной, но и многомерной -
, полученных в п независимых случайных испытаниях.
Число полученных наблюдений п называется объемом выборки.
Образно можно представить процесс получения случайной выборки как извлечение
наудачу значений из гипотетической бесконечной генеральной
совокупности, где разные значения содержатся в пропорциях,
соответствующих распределению случайной величины, и тщательно перемешаны между
собой. Случайная величина может быть не только одномерной, но и многомерной -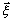 , тогда каждая из
компонент выборки
, тогда каждая из
компонент выборки 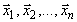 будет вектором.
будет вектором.
Конкретная случайная выборка - это просто набор
значений случайной величины (скалярных или векторных). Однако при оценке
информации, которую несет эта выборка, мы должны рассматривать ее как одну из
бесконечного числа потенциально возможных выборок объема п, т. е. как
векторную п-мерную случайную величину
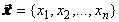
(очевидно, что в случае векторной
случайной величины 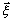 компоненты
компоненты 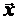 сами будут векторными случайными величинами, однако во
избежание чрезмерного усложнения обозначений мы пока ограничимся одномерным
случаем). Из условий получения выборки следует, что случайные величины
сами будут векторными случайными величинами, однако во
избежание чрезмерного усложнения обозначений мы пока ограничимся одномерным
случаем). Из условий получения выборки следует, что случайные величины 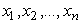 имеют
одинаковые функции распределения F(x), совпадающие с функцией
распределения исходной случайной величины
имеют
одинаковые функции распределения F(x), совпадающие с функцией
распределения исходной случайной величины 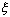 . Кроме
того, случайные величины
. Кроме
того, случайные величины 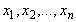 по
определению случайной выборки независимы, поэтому их совместная функция
распределения равна произведению одномерных функций распределения
по
определению случайной выборки независимы, поэтому их совместная функция
распределения равна произведению одномерных функций распределения
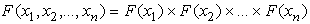
Как правило, информация, содержащаяся в
выборке, интересует нас не столько сама по себе, сколько как информация обо
всей генеральной совокупности. Однако чтобы отвечать этой цели, выборка должна
быть правильно организованной и представительной. Существует специальный раздел
математической статистики - планирование выборочных обследований.
Мы будем рассматривать только один способ получения выборки - простой
случайный выбор. В принципе схема его проста: из тщательно перемешанной
генеральной совокупности извлекается наудачу п значений. На практике,
однако, дело обстоит сложнее. Предположим, что мы отловили п взрослых
животных определенного вида и измерили их массу. Какую генеральную совокупность
представляет эта выборка? Всех животных данного вида, т. е. живущих в разных
местах, прошлых и будущих? Или популяцию, обитающую в данной местности? Или
популяцию, обитающую в данной местности в данный год? Конечно, чем уже мы будем
понимать генеральную совокупность, описываемую данной выборкой, тем ближе мы
будем к истине, но, возможно, тем меньший интерес для нас она будет
представлять.
1.2.
Характеристики случайной выборки
Итак, мы имеем случайную выборку х1,...,xn
значений случайной величины 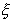 с неизвестным распределением F(x).
Как нам разумно распорядиться этими значениями, чтобы получить представление о
распределении F(x), т.е. о генеральной совокупности, из
которой извлечена эта выборка?
с неизвестным распределением F(x).
Как нам разумно распорядиться этими значениями, чтобы получить представление о
распределении F(x), т.е. о генеральной совокупности, из
которой извлечена эта выборка?
Можно использовать следующий
эвристический принцип - будем считать, что исследуемая нами генеральная
совокупность близка к гипотетической генеральной совокупности, состоящей только
из значений х1,...,xn, содержащихся в ней в
равной пропорции, т.е. случайная величина 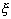 близка к случайной величине
близка к случайной величине 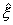 ,
принимающей п значений х1,...,xn с
вероятностями 1/n (это, действительно, максимум информации о значениях
случайной величины и их вероятностях, которую можно извлечь из выборки).
Распределение случайной величины
,
принимающей п значений х1,...,xn с
вероятностями 1/n (это, действительно, максимум информации о значениях
случайной величины и их вероятностях, которую можно извлечь из выборки).
Распределение случайной величины 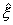 называется эмпирическим распределением случайной величины
называется эмпирическим распределением случайной величины 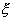 , а ее функция распределения
, а ее функция распределения 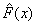 - эмпирической
функцией распределения. Очевидно, что каждой выборке соответствует своя
эмпирическая функция распределения, т.е. можно сказать, что
- эмпирической
функцией распределения. Очевидно, что каждой выборке соответствует своя
эмпирическая функция распределения, т.е. можно сказать, что 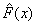 - случайная
функция.
- случайная
функция. 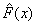 представляет
собой ступенчатую функцию, возрастающую от 0 до 1 со скачками высотой 1/n
в точках х1,...,xn (очевидно, если
некоторое значение повторяется k раз, то ему будет соответствовать один
скачок величиной k/n). Можно определить эмпирическую функцию
формулой
представляет
собой ступенчатую функцию, возрастающую от 0 до 1 со скачками высотой 1/n
в точках х1,...,xn (очевидно, если
некоторое значение повторяется k раз, то ему будет соответствовать один
скачок величиной k/n). Можно определить эмпирическую функцию
формулой 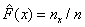 ,
где nx - число значений выборки, не
превосходящих х.
,
где nx - число значений выборки, не
превосходящих х.
Пример. Пусть случайная величина 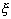 - это длина лепестка
случайно выбранного цветка ириса разноцветного (Iris versicolor). Следующий ряд чисел содержит значения
длин (в см) пятидесяти случайно выбранных лепестков:
- это длина лепестка
случайно выбранного цветка ириса разноцветного (Iris versicolor). Следующий ряд чисел содержит значения
длин (в см) пятидесяти случайно выбранных лепестков:
Таблица 1
|
4.6
|
4.5
|
4.8
|
4.6
|
5.1
|
3.9
|
4.5
|
4.7
|
4.7
|
4.5
|
|
4
|
3.8
|
4.5
|
4
|
4.4
|
4.4
|
4.5
|
4.1
|
4.5
|
3.5
|
|
4.2
|
3.3
|
4.2
|
4.2
|
4.6
|
3.9
|
4.5
|
3.5
|
3.7
|
3.9
|
|
4.3
|
4.2
|
4
|
4.7
|
4.4
|
4.1
|
4.9
|
4.7
|
4.3
|
3
|
|
4.1
|
4.7
|
3.6
|
4.9
|
4
|
4
|
4.4
|
4.8
|
5
|
3.3
|
Упорядочим эти значения по величине, т.е.
представим их в виде так называемого вариационного ряда:
Таблица 2
|
3
|
3.3
|
3.3
|
3.5
|
3.5
|
3.6
|
3.7
|
3.8
|
3.9
|
3.9
|
|
3.9
|
4
|
4
|
4
|
4
|
4
|
4.1
|
4.1
|
4.1
|
4.2
|
|
4.2
|
4.2
|
4.2
|
4.3
|
4.3
|
4.4
|
4.4
|
4.4
|
4.4
|
4.5
|
|
4.5
|
4.5
|
4.5
|
4.5
|
4.5
|
4.5
|
4.6
|
4.6
|
4.6
|
4.7
|
|
4.7
|
4.7
|
4.7
|
4.7
|
4.8
|
4.8
|
4.9
|
4.9
|
5
|
5.1
|
На рис. 1 представлено эмпирическое
распределение случайной величины 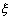 , для этой выборки, т.е. распределение случайной величины
, для этой выборки, т.е. распределение случайной величины 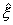 , а на рис. 2 - соответствующая эмпирическая функция
распределения
, а на рис. 2 - соответствующая эмпирическая функция
распределения 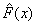 .
.
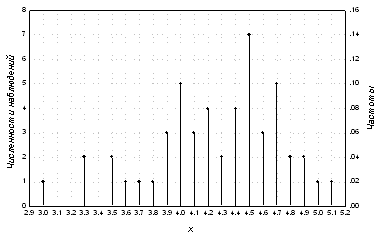
Рис.1. Пример эмпирического
распределения.
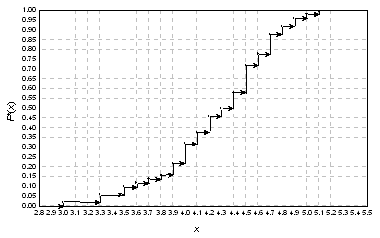
Рис.2. Пример
эмпирической функции распределения.
Поскольку эмпирическая функция
распределения 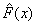 является оценкой для F(x)
(можно доказать, что при
является оценкой для F(x)
(можно доказать, что при 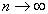 вероятность того, что максимальное расхождение между
вероятность того, что максимальное расхождение между 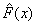 и F(x)
не превзойдет заданного малого числа
и F(x)
не превзойдет заданного малого числа 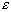 , стремится
к единице), можно взять характеристики
, стремится
к единице), можно взять характеристики 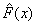 в качестве оценок характеристик
генерального распределения.
в качестве оценок характеристик
генерального распределения.
Ниже мы приводим полученные таким образом
формулы для некоторых выборочных характеристик.
|
Название
характеристики
|
Формула
|
|
Выборочный момент порядка k
|
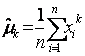
|
|
Выборочный центральный момент
Порядка k
|
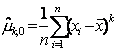
|
|
Выборочное
среднее - первый нецентральный момент
|
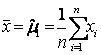
|
|
Выборочная
дисперсия - (см. в главе 2 обоснование деления на n-1 вместо деления на n)
|
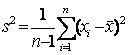
|
|
Выборочный
коэффициент асимметрии
|
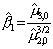
|
|
Выборочный
коэффициент эксцесса
|
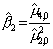
|
Зная эмпирическую функцию распределения,
можно найти эмпирические квантили, квартили и итерквартильную широту точно так
же, как в случае обычной (теоретической) функции распределения. А именно,
выборочная квантиль 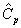 порядка р получается как
абсцисса точки пересечения горизонтальной прямой, пересекающей ось ординат в
точке р, с эмпирической функцией распределения
порядка р получается как
абсцисса точки пересечения горизонтальной прямой, пересекающей ось ординат в
точке р, с эмпирической функцией распределения 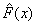 (если пересечение не
точка, а отрезок, то в качестве квантили можно взять абсциссу середины этого
отрезка). Выборочные квантили
(если пересечение не
точка, а отрезок, то в качестве квантили можно взять абсциссу середины этого
отрезка). Выборочные квантили 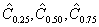 дают соответственно выборочную
нижнюю квартиль
дают соответственно выборочную
нижнюю квартиль 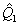 ,
выборочную медиану
,
выборочную медиану 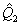 и выборочную верхнюю квартиль
и выборочную верхнюю квартиль 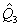 , а разность
, а разность 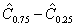 - выборочную интерквартильную
широту. Еще одна характеристика разброса значений случайной величины - размах R
определяется как разность между максимальным и минимальным значением в выборке.
- выборочную интерквартильную
широту. Еще одна характеристика разброса значений случайной величины - размах R
определяется как разность между максимальным и минимальным значением в выборке.
Если наблюдается не одномерная, а
двумерная случайная величина 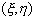 , т. е. выборка состоит из п пар
значений {x1,y1},{x2,y2},…,{xn,yn}, то можно вычислить выборочный
коэффициент ковариации для
, т. е. выборка состоит из п пар
значений {x1,y1},{x2,y2},…,{xn,yn}, то можно вычислить выборочный
коэффициент ковариации для 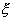 и
и 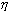
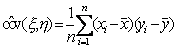
где
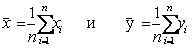
Выборочный коэффициент корреляции
определяется формулой
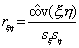
где
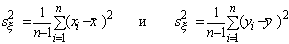
Выборочную моду xmod целесообразно оценивать для дискретного
и непрерывного генерального распределения различными способами. В дискретном
случае оценкой моды будет значение, встретившееся в выборке наибольшее число
раз.
Ниже даны значения характеристик, вычисленные
для приведенного выше примера данных о длинах лепестков ириса.
|
Название
характеристики
|
Значение
характеристики
|
|
Выборочное среднее
|
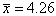
|
|
Выборочная дисперсия
|
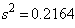
|
|
Выборочный
коэффициент асимметрии
|
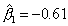
|
|
Выборочный
коэффициент эксцесса
|
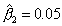
|
|
Минимум
|
xmin=3.0
|
|
Максимум
|
xmax=5.1
|
|
Размах
|
R=2.1
|
|
Нижняя
квартиль
|
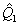 =4.00 =4.00
|
|
Верхняя
квартиль
|
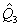 =4.60 =4.60
|
|
Интерквартильный
размах
|
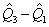 =0.60 =0.60
|
|
Медиана
|
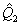 =4.35 =4.35
|
|
Мода
|
xmod=4.50
|
В непрерывном случае повторяющиеся
значения редки или вообще отсутствуют, поэтому следует разбить диапазон
изменения наблюденных значений точками a0, a1,...,
ak на k равных промежутков [a0, a1],
(a1, a2], ..., (ak-1, ak]
длиной h=(ak-a0)/k и в качестве выборочной моды взять середину интервала, в который
попало наибольшее число значений.
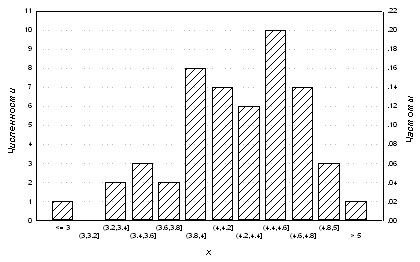
Рис.3. Пример
гистограммы.
Результаты разбиения диапазона изменения
значений выборки на интервалы и последующего подсчета числа значений ni, попавших в интервалы i=1, 2, …, k, можно представить графически. Построив
над каждым интервалом i столбик высотой ni, мы получим так называемую гистограмму.
Если при построении гистограммы оперировать не числом значений, попавших в
интервалы, а их относительной частотой в выборке 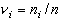 и откладывать
столбики высотой
и откладывать
столбики высотой 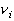 , то
полученная гистограмма будет выборочным аналогом плотности непрерывного
распределения. В частности, сумма площадей всех столбиков гистограммы будет
равна единице, как и для плотности распределения. Очевидно, что поскольку частоты
, то
полученная гистограмма будет выборочным аналогом плотности непрерывного
распределения. В частности, сумма площадей всех столбиков гистограммы будет
равна единице, как и для плотности распределения. Очевидно, что поскольку частоты
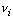 пропорциональны численностям ni, гистограммы для численностей и частот
различаются только масштабом шкалы по оси ординат. На рис. 3 приведен пример
гистограммы для рассмотренной выше выборки, содержащей 50 длин лепестков ириса
(заметим, что рис. 3 можно рассматривать как результат преобразования рис. 1
путем группировки значений по оси ординат).
пропорциональны численностям ni, гистограммы для численностей и частот
различаются только масштабом шкалы по оси ординат. На рис. 3 приведен пример
гистограммы для рассмотренной выше выборки, содержащей 50 длин лепестков ириса
(заметим, что рис. 3 можно рассматривать как результат преобразования рис. 1
путем группировки значений по оси ординат).
При построении гистограммы возникает
трудно формализуемая проблема выбора оптимальных длин интервалов разбиения h. Обычно число интервалов разбиения
выбирают из расчета, чтобы в каждый интервал попало в среднем не менее десяти
наблюдений (при очень малых объемах выборки это число уменьшают). Таким
образом, при увеличении объема выборки п можно уменьшать длины
интервалов разбиения и более детально характеризовать выборку, а следовательно,
и порождающее ее генеральное распределение. По сравнению с эмпирической
функцией распределения гистограмма более наглядна, однако при ее построении
привносится элемент субъективизма.
2. СТАТИСТИЧЕСКОЕ
ОЦЕНИВАНИЕ
2.1. Логика
статистического оценивания
Допустим, что у нас имеется случайная
выборка х1,х2,...,xn значений
некоторой случайной величины 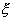 . Распределение этой случайной величины может быть либо
полностью неизвестным, либо частично известным, например, может быть известна
функциональная форма его распределения (вид функции распределения или плотности
в непрерывном случае и формулы, определяющей вероятности отдельных значений, -
в дискретном). Если распределение неизвестно, то нас могут интересовать
различные его характеристики - математическое ожидание, мода, медиана,
дисперсия, интерквартильная широта, моменты, асимметрия, эксцесс и т.д. Если
вид распределения известен, а неизвестны лишь значения определяющих его
параметров, нас могут интересовать также (или даже прежде всего) значения этих
параметров, например, параметров
. Распределение этой случайной величины может быть либо
полностью неизвестным, либо частично известным, например, может быть известна
функциональная форма его распределения (вид функции распределения или плотности
в непрерывном случае и формулы, определяющей вероятности отдельных значений, -
в дискретном). Если распределение неизвестно, то нас могут интересовать
различные его характеристики - математическое ожидание, мода, медиана,
дисперсия, интерквартильная широта, моменты, асимметрия, эксцесс и т.д. Если
вид распределения известен, а неизвестны лишь значения определяющих его
параметров, нас могут интересовать также (или даже прежде всего) значения этих
параметров, например, параметров 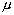 и
и 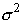 в случае нормального распределения, параметра
в случае нормального распределения, параметра 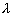 - в случае пуассоновского, параметра p - в случае биномиального. Задача
оценивания неизвестного параметра или характеристики
- в случае пуассоновского, параметра p - в случае биномиального. Задача
оценивания неизвестного параметра или характеристики 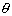 распределения
случайной величины
распределения
случайной величины 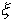 состоит в вычислении на основе
значений выборки х1,х2,...,xn
величины
состоит в вычислении на основе
значений выборки х1,х2,...,xn
величины 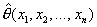 , в каком-то смысле близкой к оцениваемому параметру или
характеристике и называемой точечной оценкой
, в каком-то смысле близкой к оцениваемому параметру или
характеристике и называемой точечной оценкой 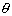 .
.
Фактически мы решали задачу оценивания в
предыдущем разделе, поскольку рассматривали выборочные математическое ожидание,
дисперсию и т.д. как оценки неизвестных генеральных характеристик. Однако этот
подход к оцениванию был скорее интуитивным, и сейчас мы попробуем его
формализовать. Эта формализация касается уточнения смысла близости выборочной
оценки 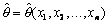 к
оцениваемому параметру
к
оцениваемому параметру 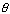 . Заметим,
прежде всего, что
. Заметим,
прежде всего, что 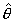 является
случайной величиной, значения которой меняются от выборки к выборке. Для
некоторых выборок значение
является
случайной величиной, значения которой меняются от выборки к выборке. Для
некоторых выборок значение 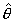 может
оказаться очень близким к оцениваемому параметру
может
оказаться очень близким к оцениваемому параметру 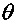 ,
для других - довольно далеким. Можно, однако, потребовать, что хотя бы в
среднем оценки для разных выборок группировались вокруг оцениваемого параметра,
т.е. чтобы выполнялось условие
,
для других - довольно далеким. Можно, однако, потребовать, что хотя бы в
среднем оценки для разных выборок группировались вокруг оцениваемого параметра,
т.е. чтобы выполнялось условие  . Оценки,
удовлетворяющие этому условию называются несмещенными. Отметим,
что в зависимости от контекста мы рассматриваем
. Оценки,
удовлетворяющие этому условию называются несмещенными. Отметим,
что в зависимости от контекста мы рассматриваем 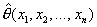 либо
как случайную величину (и только в этом случае мы имеем право говорить о
математическом ожидании
либо
как случайную величину (и только в этом случае мы имеем право говорить о
математическом ожидании 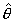 - как это
было в приведенном определении несмещенности), либо как алгебраическую формулу
для вычисления значения оценки по выборке, либо просто как конкретное значение,
полученное для конкретной выборки.
- как это
было в приведенном определении несмещенности), либо как алгебраическую формулу
для вычисления значения оценки по выборке, либо просто как конкретное значение,
полученное для конкретной выборки.
Можно доказать, пользуясь свойствами
математического ожидания и определением выборки, что выборочное математическое
ожидание (чаще используется термин выборочное среднее) 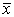 является несмещенной оценкой генерального среднего
является несмещенной оценкой генерального среднего 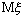 . Действительно,
имеем
. Действительно,
имеем
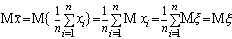
(мы воспользовались также тем очевидным
фактом, что распределение любой компоненты выборки xi, совпадает с распределением
анализируемой случайной величины 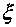 ).
).
Однако, вопреки нашей интуиции,
математическое ожидание второго центрального момента
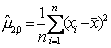
не равно генеральной дисперсии. Для
получения несмещенной оценки дисперсии надо разделить сумму квадратов на n-1, а не на n. Действительно, пользуясь свойствами математического
ожидания, в частности тем, что математическое ожидание произведения независимых
случайных величин равно произведению их математических ожиданий, получаем
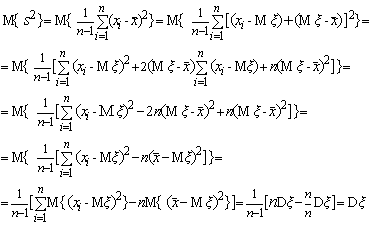
Таким образом, несмещенной оценкой для 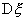 будет
будет 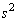 - сумма квадратов
отклонений от среднего, деленная на n-1
- сумма квадратов
отклонений от среднего, деленная на n-1
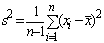
Следует, однако, отметить, что хотя
выборочный центральный момент второго порядка не является несмещенной оценкой
для дисперсии 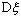 ,
его смещение (отклонение математического ожидания от оцениваемого параметра
,
его смещение (отклонение математического ожидания от оцениваемого параметра 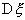 ), равное
), равное 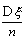 , стремится
к нулю при
, стремится
к нулю при 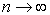 . Оценки,
удовлетворяющие этому свойству, называются асимптотически несмещенными,
и часто, когда не удается найти несмещенной оценки для оцениваемого параметра,
довольствуются асимптотически несмещенными оценками. Конечно, нас не очень интересует,
что происходит со смещением при
. Оценки,
удовлетворяющие этому свойству, называются асимптотически несмещенными,
и часто, когда не удается найти несмещенной оценки для оцениваемого параметра,
довольствуются асимптотически несмещенными оценками. Конечно, нас не очень интересует,
что происходит со смещением при 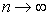 , когда мы
имеем дело с конкретной выборкой фиксированного объема n. Скорее, мы предпочитаем асимптотически
несмещенные оценки из-за того, что, как правило, их смещение относительно
невелико при не очень малых объемах выборки. Например, смещение
, когда мы
имеем дело с конкретной выборкой фиксированного объема n. Скорее, мы предпочитаем асимптотически
несмещенные оценки из-за того, что, как правило, их смещение относительно
невелико при не очень малых объемах выборки. Например, смещение 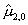 при n=50 равно 2% .
при n=50 равно 2% .
Конечно, коль скоро 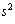 есть несмещенная оценка
для
есть несмещенная оценка
для 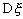 , то ей и
следует пользоваться. Однако нас чаще интересует не столько оценка дисперсии
, то ей и
следует пользоваться. Однако нас чаще интересует не столько оценка дисперсии 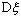 случайной величины x, сколько оценка ее среднеквадратичного отклонения
случайной величины x, сколько оценка ее среднеквадратичного отклонения 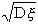 . Естественно
взять в качестве оценки среднеквадратичного отклонения квадратный корень
несмещенной оценки, т.е. s, однако следует помнить, что s не будет несмещенной оценкой для
. Естественно
взять в качестве оценки среднеквадратичного отклонения квадратный корень
несмещенной оценки, т.е. s, однако следует помнить, что s не будет несмещенной оценкой для 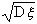 , а будет лишь асимптотически
несмещенной.
, а будет лишь асимптотически
несмещенной.
Итак, на примере с получением несмещенной
оценки дисперсии мы убедились, что "естественный" способ получения
оценок, состоящий в использовании характеристик выборочного распределения в
качестве оценок характеристик генерального распределения не всегда приводит к
наилучшим результатам. Существуют ряд регулярных приемов получения оценок
(метод моментов, метод максимального правдоподобия, метод минимума хи-квадрата),
но они не всегда приводят к наилучшим оценкам (например, с точки зрения несмещенности).
Поэтому общий подход к задаче оценивания состоит в том, что в качестве
претендента на оценку характеристики или параметра (для краткости мы иногда
будем использовать только термин "параметр") 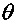 генерального распределения по случайной выборке х1,х2,...,xn
в принципе может претендовать любая функция
генерального распределения по случайной выборке х1,х2,...,xn
в принципе может претендовать любая функция 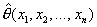 от
компонент выборки (часто вместо словосочетания "функция от выборки"
используют более краткий термин "статистика"), среди
которых должна быть выбрана наилучшая.
от
компонент выборки (часто вместо словосочетания "функция от выборки"
используют более краткий термин "статистика"), среди
которых должна быть выбрана наилучшая.
У нас уже есть один критерий для
сравнения оценок - это наличие или отсутствие несмещенности (хотя бы
асимптотической). Однако этого недостаточно. Действительно, было показано, что
выборочное среднее 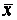 - несмещенная оценка для математического
ожидания
- несмещенная оценка для математического
ожидания 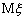 . Но можно
предложить другие несмещенные оценки для математического ожидания. Например, полусумма
первого и последнего значений выборки (х1+xn)/2
как легко показать, будет также несмещенной оценкой для
. Но можно
предложить другие несмещенные оценки для математического ожидания. Например, полусумма
первого и последнего значений выборки (х1+xn)/2
как легко показать, будет также несмещенной оценкой для 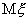 . Конечно, интуитивно мы чувствуем, что
. Конечно, интуитивно мы чувствуем, что 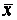 - более предпочтительная оценка, поскольку она более полно учитывает
информацию, содержащуюся в выборке. Однако необходим какой-то критерий,
позволяющий чисто формально показать, что
- более предпочтительная оценка, поскольку она более полно учитывает
информацию, содержащуюся в выборке. Однако необходим какой-то критерий,
позволяющий чисто формально показать, что 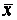 лучше оценок типа (х1+xn)/2.
Таким критерием, может служить состоятельность оценки. Оценка
лучше оценок типа (х1+xn)/2.
Таким критерием, может служить состоятельность оценки. Оценка 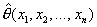 называется
состоятельной, если при
называется
состоятельной, если при 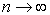 она
сходится по вероятности к оцениваемому параметру
она
сходится по вероятности к оцениваемому параметру 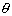 ,
т.е. если для любого положительного
,
т.е. если для любого положительного 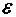 выполняется
условие
выполняется
условие
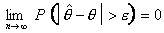
Достаточным условием состоятельности оценки 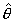 является
ее несмещенность и стремление дисперсии оценки
является
ее несмещенность и стремление дисперсии оценки 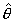 к
нулю при увеличении объема выборки, т.е. оценка будет состоятельной, если
к
нулю при увеличении объема выборки, т.е. оценка будет состоятельной, если  и
и 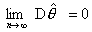 . Справедливость этого утверждения
непосредственно следует из неравенства Чебышева, которое в данном случае имеет
следующий вид
. Справедливость этого утверждения
непосредственно следует из неравенства Чебышева, которое в данном случае имеет
следующий вид
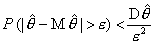
Пользуясь этим достаточным условием,
покажем, что выборочное среднее 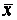 является состоятельной оценкой математического ожидания. Поскольку
несмещенность
является состоятельной оценкой математического ожидания. Поскольку
несмещенность 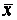 уже была доказана, осталось показать, что
уже была доказана, осталось показать, что
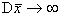 при
при 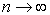 . Действительно, имеем
. Действительно, имеем
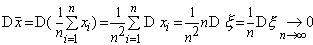
Таким образом 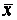 - состоятельная оценка для математического ожидания
- состоятельная оценка для математического ожидания 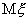 случайной
величины
случайной
величины 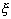 . Однако легко видеть, что полусумма (х1+xn)/2
первого и последнего значений выборки, будучи несмещенной, не является
состоятельной, поскольку ее дисперсия не стремится к 0 при неограниченном
увеличении n
. Однако легко видеть, что полусумма (х1+xn)/2
первого и последнего значений выборки, будучи несмещенной, не является
состоятельной, поскольку ее дисперсия не стремится к 0 при неограниченном
увеличении n
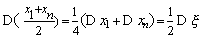
Аналогично можно доказать, что
несмещенная оценка дисперсии s2 является состоятельной оценкой для генеральной дисперсии 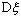 .
.
Еще одним желательным свойством оценки
является ее эффективность. Несмещенная оценка 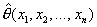 параметра
параметра 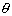 называется
эффективной оценкой, если
называется
эффективной оценкой, если 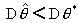 для любой другой несмещенной оценки
для любой другой несмещенной оценки 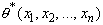 . Дело в том, что две оценки, будучи обе несмещенными и
состоятельными, могут различаться своими дисперсиями. Например, следующая
оценка для математического ожидания
. Дело в том, что две оценки, будучи обе несмещенными и
состоятельными, могут различаться своими дисперсиями. Например, следующая
оценка для математического ожидания
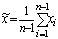
будет, как легко проверить, несмещенной и
состоятельной. Однако она не будет эффективной, т.к. ее дисперсия 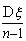 больше
дисперсии
больше
дисперсии 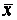 , которая равна
, которая равна 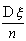 .
.
2.2.
Доверительные интервалы
Оценки, которые рассматривались в
предыдущем параграфе, принято называть точечными, поскольку за
оценку неизвестного параметра 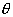 принимается конкретное значение (точка), вычисляемое по
выборке (например, значение выборочного среднего в качестве оценки для
математического ожидания). Однако часто нас интересует не только конкретное
значение, но и такие свойства оценки, которые ассоциируются с ее точностью и
надежностью. Этим требованиям отвечают так называемые интервальные оценки. Интервальная
оценка - это некоторый интервал
принимается конкретное значение (точка), вычисляемое по
выборке (например, значение выборочного среднего в качестве оценки для
математического ожидания). Однако часто нас интересует не только конкретное
значение, но и такие свойства оценки, которые ассоциируются с ее точностью и
надежностью. Этим требованиям отвечают так называемые интервальные оценки. Интервальная
оценка - это некоторый интервал 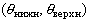 , где
, где 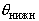 и
и 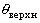 есть функции от выборочных значений
и
есть функции от выборочных значений
и 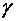 :
: 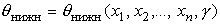 ,
, 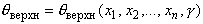 , называемый доверительным,
который с заданной (достаточно высокой) вероятностью
, называемый доверительным,
который с заданной (достаточно высокой) вероятностью 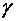 ,
называемой доверительной, содержит истинное значение
,
называемой доверительной, содержит истинное значение 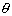 оцениваемого
неизвестного параметра (случайные величины
оцениваемого
неизвестного параметра (случайные величины 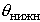 и
и 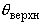 называются, соответственно, верхним
и нижним доверительными пределами), т.е.
называются, соответственно, верхним
и нижним доверительными пределами), т.е.
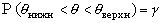
(дополнение 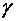 до 1 будем
обозначать
до 1 будем
обозначать 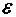 , т.е.
, т.е. 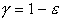 ). Наиболее
часто используются значения доверительной вероятности
). Наиболее
часто используются значения доверительной вероятности 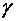 равные 0.95 или 0.99 (95%-ный и 99%-ный доверительные
интервалы).
равные 0.95 или 0.99 (95%-ный и 99%-ный доверительные
интервалы).
2.2.1.
Доверительный интервал для математического ожидания нормально распределенной
случайной величины с известной дисперсией
Проще всего понять логику интервального
оценивания на примере построения доверительного интервала для математического
ожидания нормально распределенной случайной величины с известной дисперсией.
Пусть 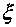 -
нормально распределенная случайная величина с неизвестным математическим
ожиданием
-
нормально распределенная случайная величина с неизвестным математическим
ожиданием 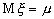 и
дисперсией
и
дисперсией 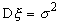 , т.е. в
наших обозначениях
, т.е. в
наших обозначениях 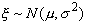 , и имеется
выборка значений этой случайной величины х1,х2,...,xn
объема n. Требуется найти доверительный интервал
для
, и имеется
выборка значений этой случайной величины х1,х2,...,xn
объема n. Требуется найти доверительный интервал
для 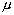 с
доверительной вероятностью
с
доверительной вероятностью 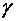 .
.
Выше было показано, что выборочное
среднее (для любого распределения, в том числе и нормального) имеет
математическое ожидание, равное математическому ожиданию исходной случайной
величины, т.е. 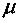 ,
а дисперсия - дисперсии исходной случайной величины, деленной на n, т.е.
,
а дисперсия - дисперсии исходной случайной величины, деленной на n, т.е. 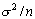 .
Следовательно, статистика
.
Следовательно, статистика

полученная путем стандартизации
выборочного среднего 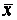 , будет иметь нулевое математическое ожидание
и единичную дисперсию. Поскольку, как мы знаем, линейные комбинации нормально
распределенных случайных величин имеют также нормальное распределение, а
случайная величина u
фактически является линейной комбинацией нормально распределенных случайных величин
х1,х2,...,xn, то u будет стандартно распределенной
случайной величиной, т.е.
, будет иметь нулевое математическое ожидание
и единичную дисперсию. Поскольку, как мы знаем, линейные комбинации нормально
распределенных случайных величин имеют также нормальное распределение, а
случайная величина u
фактически является линейной комбинацией нормально распределенных случайных величин
х1,х2,...,xn, то u будет стандартно распределенной
случайной величиной, т.е. 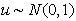 . Стандартное нормальное распределение - это конкретное,
полностью заданное распределение, квантили которого можно найти в
соответствующих таблицах (или вычислить путем численного интегрирования). В
частности, можно найти симметричные относительно центра распределения границы,
внутрь которых u попадает
с заданной вероятностью g
. Стандартное нормальное распределение - это конкретное,
полностью заданное распределение, квантили которого можно найти в
соответствующих таблицах (или вычислить путем численного интегрирования). В
частности, можно найти симметричные относительно центра распределения границы,
внутрь которых u попадает
с заданной вероятностью g
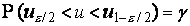
или, с учетом симметрии,
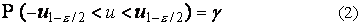
(через 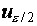 и
и 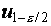 обозначены квантили стандартного
нормального распределения порядка
обозначены квантили стандартного
нормального распределения порядка 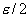 и
и 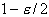 ). В частности, справедливы следующие
неравенства
). В частности, справедливы следующие
неравенства
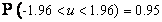 и
и 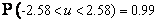
Подставляя в (2) выражение для u из (1), получаем
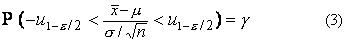
или, после преобразований,
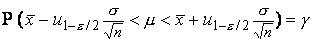
Это означает, что интервал 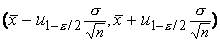 будет
будет 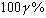 -ным доверительным
интервалом для неизвестного математического ожидания
-ным доверительным
интервалом для неизвестного математического ожидания 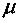 нормального распределения
с известной дисперсией
нормального распределения
с известной дисперсией 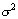 . В частности, 95%-ным доверительным
интервалом будет интервал
. В частности, 95%-ным доверительным
интервалом будет интервал 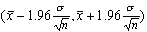 , а 99%-ным -
, а 99%-ным - 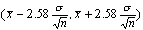 . Мы видим, что
доверительный интервал уменьшается при уменьшении
. Мы видим, что
доверительный интервал уменьшается при уменьшении 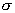 , увеличении объема выборки и
снижении доверительной вероятности.
, увеличении объема выборки и
снижении доверительной вероятности.
2.2.2.
Доверительный интервал для математического ожидания нормально распределенной
случайной величины с неизвестной дисперсией
В случае неизвестной дисперсии постановка
задачи и ход рассуждений при построении доверительного интервала аналогичны
случаю известной дисперсии, рассмотренному в предыдущем параграфе. Разница
состоит в том, что в выражении (1) неизвестное среднеквадратичное отклонение  заменяется на его
выборочную оценку s
заменяется на его
выборочную оценку s

Полученная таким путем статистика t, будучи довольно сложной функцией от
нормально распределенных случайных величин х1,х2,...,xn,
уже не будет нормально распределенной. Можно доказать, что t имеет t
-распределение Стьюдента с n-1
степенями свободы. Отсюда следует, что справедливо равенство
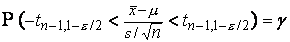
аналогичное уравнению (3) и отличающееся
от него заменой 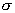 на
s и квантилей нормального распределения на
соответствующие квантили t
-распределения с n-1
степенями свободы. Соответственно
на
s и квантилей нормального распределения на
соответствующие квантили t
-распределения с n-1
степенями свободы. Соответственно 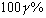 -ный доверительный
интервал для неизвестного математического ожидания
-ный доверительный
интервал для неизвестного математического ожидания 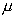 нормального распределения
с неизвестной дисперсией
нормального распределения
с неизвестной дисперсией 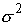 будет иметь следующий вид
будет иметь следующий вид
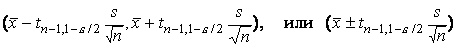
Известно, что этот доверительный интервал
и доверительный интервал из предыдущего раздела являются робастными,
т.е. они нечувствительны к умеренным отклонениям от предположения о
нормальности распределения. Во всяком случае, как отмечается в пособиях по
математической статистике, при объеме выборки не менее 15 становится
целесообразно использовать приведенные доверительные интервалы для
математического ожидания и в случае умеренного отклонения от предположения о
нормальности.
Заметим, что при  t-распределение приближается к нормальному
распределению, а его квантили - к квантилям нормального распределения. Например,
при n-1=60 квантиль
t-распределение приближается к нормальному
распределению, а его квантили - к квантилям нормального распределения. Например,
при n-1=60 квантиль 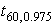 равна 2.00, что не очень
сильно отличается от аналогичного значения
равна 2.00, что не очень
сильно отличается от аналогичного значения  для нормального распределения
(особенно на фоне выборочных флуктуаций
для нормального распределения
(особенно на фоне выборочных флуктуаций 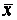 и s). Поэтому при числе наблюдений порядка
нескольких десятков можно пользоваться нормальным приближением для t-распределения. Однако при небольшом
числе степеней свободы различие между квантилями t-распределения и нормального распределения довольно
значительно. Например, для n-1=1 имеем
и s). Поэтому при числе наблюдений порядка
нескольких десятков можно пользоваться нормальным приближением для t-распределения. Однако при небольшом
числе степеней свободы различие между квантилями t-распределения и нормального распределения довольно
значительно. Например, для n-1=1 имеем
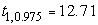 , для n-1=2 -
, для n-1=2 - 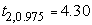 , для n-1=5 -
, для n-1=5 - 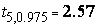 . При n-1=9 (выборка из 10 наблюдений) получаем значение
. При n-1=9 (выборка из 10 наблюдений) получаем значение 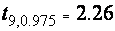 , что уже не
очень сильно отличается от 1.96.
, что уже не
очень сильно отличается от 1.96.
Возвращаясь к примеру с длинами лепестков
ириса и учитывая, что 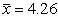 , s=0.47,
, s=0.47, 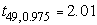 (при числе степеней свободы n-1=49), а также предполагая, что
распределение длин лепестков нормально (в следующем разделе мы рассмотрим
процедуру проверки этого предположения), получаем, что 95%-ным доверительным
интервалом для математического ожидания длины лепестка будет интервал (4.13, 4.39).
Т.е. мы можем утверждать, что с вероятностью 0.95 неизвестное
(при числе степеней свободы n-1=49), а также предполагая, что
распределение длин лепестков нормально (в следующем разделе мы рассмотрим
процедуру проверки этого предположения), получаем, что 95%-ным доверительным
интервалом для математического ожидания длины лепестка будет интервал (4.13, 4.39).
Т.е. мы можем утверждать, что с вероятностью 0.95 неизвестное 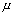 находится
между 4.13 и 4.39 (точнее следует сказать, что найденный доверительный интервал
с вероятностью 0.95 накроет неизвестное значение
находится
между 4.13 и 4.39 (точнее следует сказать, что найденный доверительный интервал
с вероятностью 0.95 накроет неизвестное значение 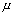 ).
).
2.2.3.
Доверительный интервал для неизвестной дисперсии нормально распределенной
случайной величины (при неизвестном математическом ожидании)
Для нахождения доверительного интервала
для неизвестной дисперсии нормально распределенной случайной величины
рассмотрим статистику
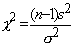
Можно показать, что эта статистика имеет c2-распределение
с п-1 степенями свободы. Следовательно, справедливо равенство
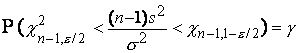
которое можно переписать в виде
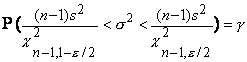
Таким образом, 100g%-ный
доверительный интервал для неизвестной дисперсии 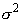 нормального распределения
с неизвестным математическим ожиданием
нормального распределения
с неизвестным математическим ожиданием 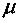 будет иметь следующий вид
будет иметь следующий вид
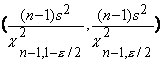
где 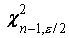 и
и 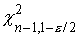 - квантили распределения c2 с
п -1 степенями свободы. В частности, для длины лепестков ириса, учитывая,
что s2 =0.22, n-1=49,
- квантили распределения c2 с
п -1 степенями свободы. В частности, для длины лепестков ириса, учитывая,
что s2 =0.22, n-1=49, 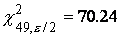 и
и 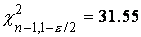 , получаем, что 95%-ным
доверительным интервалом для дисперсии (в предположении нормальности распределения) будет
интервал (0.15, 0.34).
, получаем, что 95%-ным
доверительным интервалом для дисперсии (в предположении нормальности распределения) будет
интервал (0.15, 0.34).
Заметим, что полученный доверительный
интервал для дисперсии, в отличии от доверительного интервала для
математического ожидания, чувствителен к отклонениям от исходного предположения
о нормальности распределения.
2.2.4.
Доверительный интервал для неизвестного параметра p биномиального распределения
Пусть произведено n независимых испытаний, в которых
некоторое событие A произошло k раз. Требуется найти точечную и
интервальную оценку неизвестной вероятности p появления этого события.
Эту задачу можно рассматривать в двух
эквивалентных формулировках. В первой формулировке считается, что получено n наблюдений случайной величины 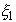 ,
принимающей с вероятностью p
значение 1 в случае появления события A и с вероятностью 1-p значение 0 - в случае непоявления события A. Во второй формулировке считается, что
имеется только одно наблюдение случайной величины
,
принимающей с вероятностью p
значение 1 в случае появления события A и с вероятностью 1-p значение 0 - в случае непоявления события A. Во второй формулировке считается, что
имеется только одно наблюдение случайной величины 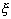 - числа появлений события A в одном сложном испытании.
- числа появлений события A в одном сложном испытании.
Поскольку математическое ожидание 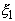 , как мы
знаем, равно p, то
получение оценки для p
равносильно получению оценки для математического ожидания
, как мы
знаем, равно p, то
получение оценки для p
равносильно получению оценки для математического ожидания 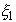 .
Несмещенной, состоятельной и эффективной оценкой для математического ожидания
является выборочное среднее, которое в данном случае совпадает с частотой
.
Несмещенной, состоятельной и эффективной оценкой для математического ожидания
является выборочное среднее, которое в данном случае совпадает с частотой 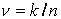 появления события A в выборке. Таким образом, выборочная частота является
несмещенной, состоятельной и эффективной оценкой для неизвестной вероятности.
Во второй формулировке математическое ожидание
появления события A в выборке. Таким образом, выборочная частота является
несмещенной, состоятельной и эффективной оценкой для неизвестной вероятности.
Во второй формулировке математическое ожидание 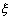 равно np, а
выборочное среднее для одного наблюдения равно самому наблюдению, т.е. k. И поскольку оценкой для np служит k (среднее по одному наблюдению), то оценкой для p снова будет k/n.
равно np, а
выборочное среднее для одного наблюдения равно самому наблюдению, т.е. k. И поскольку оценкой для np служит k (среднее по одному наблюдению), то оценкой для p снова будет k/n.
Построение доверительных интервалов
несколько проще обсуждать в терминах биномиального распределения. Можно
построить как точные доверительные интервалы для p, так и приближенные. Математическая техника нахождения
точных доверительных интервалов довольно громоздка и мы приведем здесь лишь
окончательные формулы для доверительных пределов. Напротив, выражения для
приближенных доверительных пределов легко получаются на основе применения
центральной предельной теоремы, однако они применимы лишь при достаточно
большом n - ориентировочно при 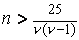 .
.
Точный
доверительный интервал
Точный доверительный интервал для
параметра биномиального распределения имеет вид
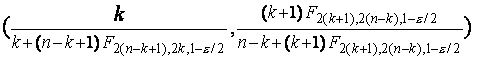
где n - число испытаний, k - число появлений события A, а 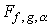 обозначает квантиль
порядка
обозначает квантиль
порядка 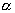 распределения F с f,
g степенями
свободы.
распределения F с f,
g степенями
свободы.
Рассмотрим в качестве примера приведенные в п. 1.2
данные о длине лепестков ириса с точки зрения оценки вероятности появления в
случайной выборке "длинных" лепестков, а именно, лепестков длиной 4.5
см и более. В данном случае n=50 и k=21.
Следовательно, точечной оценкой для p будет значение 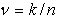 =0.42,
а 95%-ным доверительным интервалом - интервал
=0.42,
а 95%-ным доверительным интервалом - интервал
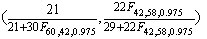
Учитывая, что F60,42,0.975 =1.78 и F42,58,0.975
=1.74, получаем окончательно интервал (0.28, 0.57).
Приближенный
доверительный интервал
Поскольку число появлений события A в n испытаниях равно сумме чисел появлений этого события в отдельных
испытаниях (0 или 1), то в соответствии с центральной предельной теоремой при
больших n распределение биномиальной случайной
величины будет близко к нормальному. Учитывая, что дисперсия биномиальной
случайной величины равна np(1-p), получаем для ее математического
ожидания np приближенные доверительные пределы 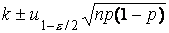 , а для параметра p - соответственно
, а для параметра p - соответственно 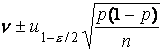 . Заменяя параметр p его выборочной оценкой
. Заменяя параметр p его выборочной оценкой 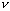 , получаем окончательно для
приближенного доверительного интервала параметра p
следующее выражение
, получаем окончательно для
приближенного доверительного интервала параметра p
следующее выражение
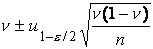 .
.
В частности, для предыдущего примера, подставляя
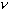 =0.42,
=0.42, 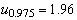 и n=50, получаем приближенный
доверительный интервал (0.28, 0.56), не слишком отличающийся от точного
доверительного интервала.
и n=50, получаем приближенный
доверительный интервал (0.28, 0.56), не слишком отличающийся от точного
доверительного интервала.
2.2.5.
Доверительный интервал для неизвестного параметра l пуассоновского распределения
Пусть число появлений некоторого события A является случайной величиной, имеющей
пуассоновское распределение, и пусть в результате наблюдения событие A произошло k раз. Требуется найти точечную и интервальную оценку
неизвестного параметра 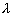 пуассоновского распределения. Поскольку
пуассоновского распределения. Поскольку 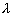 является
математическим ожиданием пуассоновской случайной величины, то несмещенной,
состоятельной и эффективной оценкой для
является
математическим ожиданием пуассоновской случайной величины, то несмещенной,
состоятельной и эффективной оценкой для 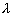 будет выборочное среднее, которое для рассматриваемой
ситуации единственного наблюдения совпадает с k. Что касается доверительных пределов для
параметра
будет выборочное среднее, которое для рассматриваемой
ситуации единственного наблюдения совпадает с k. Что касается доверительных пределов для
параметра 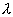 , то, как и
в случае биномиального распределения можно предложить точное и приближенное
решения. Выражения для приближенных доверительных пределов также основаны на
применении центральной предельной теоремы и применимы лишь при достаточно
большом k - ориентировочно при k>25.
, то, как и
в случае биномиального распределения можно предложить точное и приближенное
решения. Выражения для приближенных доверительных пределов также основаны на
применении центральной предельной теоремы и применимы лишь при достаточно
большом k - ориентировочно при k>25.
Точный
доверительный интервал
Точный доверительный интервал для
параметра 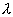 пуассоновского
распределения имеет вид
пуассоновского
распределения имеет вид
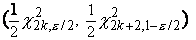
где k - число появлений события A, а 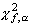 обозначает квантиль порядка
обозначает квантиль порядка 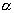 распределения
распределения 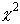 с f степенями свободы.
с f степенями свободы.
Рассмотрим следующий пример. Пусть после фильтрования
1 мл воды на фильтровальной бумаге обнаружено 100 клеток фитопланктона.
Предполагая, что число клеток в заданном объеме воды имеет пуассоновское
распределение, найти 95%-ные доверительные пределы для параметра l этого распределения. Подставляя k=100, 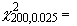 162.7 и
162.7 и 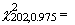 243.4 в приведенные выше выражения,
получаем 95%-ный доверительный интервал: (81.3,
121.7).
243.4 в приведенные выше выражения,
получаем 95%-ный доверительный интервал: (81.3,
121.7).
Приближенный
доверительный интервал
Поскольку число появлений события A при наблюдении пуассоновской случайной
величины 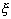 можно
аппроксимировать биномиальным распределением, а последнее - нормальным, то при
не слишком малых k в
соответствии с центральной предельной теоремой распределение случайной величины
можно
аппроксимировать биномиальным распределением, а последнее - нормальным, то при
не слишком малых k в
соответствии с центральной предельной теоремой распределение случайной величины
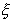 будет близко к нормальному. Учитывая, что дисперсия
пуассоновской случайной величины равна
будет близко к нормальному. Учитывая, что дисперсия
пуассоновской случайной величины равна 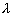 , получаем
для ее математического ожидания
, получаем
для ее математического ожидания 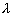 приближенные доверительные пределы
приближенные доверительные пределы 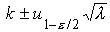 . Заменяя
параметр
. Заменяя
параметр 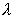 его
выборочной оценкой k, получаем
окончательно для приближенного доверительного
интервала параметра
его
выборочной оценкой k, получаем
окончательно для приближенного доверительного
интервала параметра 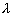 следующее выражение
следующее выражение
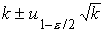 .
.
В частности, для предыдущего примера,
подставляя k=100 и 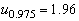 ,
получаем приближенный доверительный интервал (80.4, 119.6),
не слишком отличающийся от точного доверительного интервала.
,
получаем приближенный доверительный интервал (80.4, 119.6),
не слишком отличающийся от точного доверительного интервала.
2.2.6.
Приближенный доверительный интервал для неизвестного коэффициента корреляции
двумерного нормального распределения
Рассмотрим теперь вопрос построения
доверительного интервала для коэффициента корреляции. Пусть (х1,
y1), (х2, y2),
…, (хn,
yn) - случайная выборка объема n из двумерного нормального распределения. Пусть 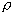 -
коэффициент корреляции случайных величин
-
коэффициент корреляции случайных величин 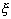 и
и 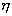 , а r - выборочный коэффициент корреляции.
Распределение самого коэффициента корреляции r, особенно при значениях
, а r - выборочный коэффициент корреляции.
Распределение самого коэффициента корреляции r, особенно при значениях 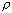 близких к 0 или 1 может сильно отличаться от нормального.
Однако следующая функция от r, называемая преобразованием Фишера,
довольно хорошо аппроксимируется нормальным распределением
близких к 0 или 1 может сильно отличаться от нормального.
Однако следующая функция от r, называемая преобразованием Фишера,
довольно хорошо аппроксимируется нормальным распределением
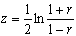
со средним 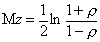 и
дисперсией
и
дисперсией 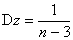 .
Соответственно, стандартизованная случайная величина будет иметь стандартное
нормальное распределение
.
Соответственно, стандартизованная случайная величина будет иметь стандартное
нормальное распределение
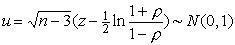
и с вероятностью 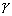 будет заключена в пределах
будет заключена в пределах 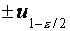 , т.е.
, т.е.
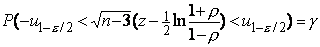
Решая неравенство под знаком вероятности
относительно неизвестного коэффициента корреляции 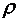 , получаем
окончательно
, получаем
окончательно
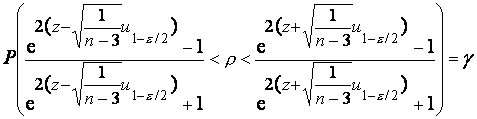
Заметим, что полученный доверительный
интервал для коэффициента корреляции чувствителен к отклонениям от исходного
предположения о двумерной нормальности случайных величин 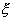 и
и 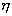 .
.
Пример. Пусть объем выборки n=10, а вычисленное по выборке значение r=0.6, тогда 95%-ным доверительным интервалом для
неизвестного коэффициента корреляции будет интервал (0.05, 0.88).


