
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ
им. М.В.
ЛОМОНОСОВА
БИОЛОГИЧЕСКИЙ
ФАКУЛЬТЕТ
В.Д. Мятлев, Л.А. Панченко, А. Т.
Терехин
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Пособие по курсу
"Математические методы в
биологии"
МОСКВА
МАКС Пресс
2002
СОДЕРЖАНИЕ
Введение
1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1.1. Случайные испытания и пространство элементарных
событий
1.2. Случайные события и операции над ними
1.3. Вероятности событий
1.4. Условная вероятность и независимость событий
1.5. Формула полной вероятности и формула Байеса
1.6. Формула Бернулли
2. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ РАСПРЕДЕЛЕНИЯ
2.1. Случайные величины
2.2. Функция распределения вероятностей случайной
величины
2.3. Дискретные случайные величины
2.4. Непрерывные случайные величины
2.5. Нормальное и связанные с ним распределения
3.
ХАРАКТЕРИСТИКИ РАСПРЕДЕЛЕНИЙ
3.1. Математическое ожидание
3.2.
Дисперсия. Среднее квадратическое отклонение. Моменты
3.3. Медиана. Мода. Квартили
3.4. Квантили
4. МНОГОМЕРНЫЕ
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ РАСПРЕДЕЛЕНИЯ
4.1. Многомерные
случайные величины и их функции
распределения
4.2. Дискретные многомерные случайные величины
4.3. Непрерывные многомерные случайные величины
ЛИТЕРАТУРА
Введение
Задача теории вероятностей состоит в
построении и анализе вероятностных математических моделей реальных явлений,
учитывающих недетерминированные, случайные аспекты этих явлений.
В биологии, ввиду сложности изучаемых ею объектов и
процессов, особенно часто приходится пользоваться вероятностными моделями.
Например, уже в такой простой задаче, как сравнение размеров самцов и самок
некоторого вида животных, мы встречаемся с той трудностью, что отдельные особи,
как самцы, так и самки, имеют разные размеры, причем некоторые самки крупнее
некоторых самцов, а некоторые самцы мельче некоторых самок.
Выход состоит в рассмотрении данной ситуации с
вероятностной точки зрения, согласно которой размеры отдельных особей
представляют собой случайно выбранные значения из двух потенциально бесконечных
множеств (генеральных совокупностей) самцов и самок данного вида.
Вероятностное описание генеральной совокупности считается
заданным, если заданы доли встречаемости элементов всех возможных размеров из
этой генеральной совокупности.
Далее мы увидим, что удобно задавать распределение
долей разных размеров с помощью некоторой функции, называемой функцией
распределения вероятностей. При таком подходе задача сравнения размеров
самцов и самок сводится к задаче сравнения соответствующих функций
распределения.
Данное пособие посвящено рассмотрению основных
понятий теории вероятностей и математических свойств вероятностных моделей.
Для проверки адекватности вероятностных моделей и их
подгонки к реально наблюдаемым данным служат методы математической
статистики, которые рассматриваются в отдельном пособии.
1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ
ВЕРОЯТНОСТЕЙ
1.1. Случайные испытания и
пространство элементарных событий
Исходным понятием теории вероятностей является
понятие случайного испытания (эквивалентные термины: опыт,
эксперимент, наблюдение), т.е. действия, приводящего к некоторому результату,
который, вообще говоря, нельзя однозначно предсказать, зная комплекс
условий проведения испытания. Например, нельзя заранее наверняка
угадать, гербом или решкой упадет подброшенная вверх монета. Нельзя однозначно
предсказать пол будущего цыпленка по внешнему виду яйца.
Предполагается, что случайное испытание в принципе
можно повторять неограниченное число раз, сохраняя комплекс условий, но
получая, вообще говоря, разные результаты.
Множество интересующих нас возможных результатов,
которые могут произойти при проведении испытания с заданным комплексом условий,
называют пространством элементарных событий (иногда используют термин -
пространство элементарных исходов). Пространство элементарных событий
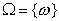 должно быть
полной системой событий, а именно, в результате испытания должно произойти
одно, и только одно, из элементарных событий.
должно быть
полной системой событий, а именно, в результате испытания должно произойти
одно, и только одно, из элементарных событий.
При бросании монеты пространство элементарных событий
состоит из двух элементарных событий: 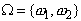 - «герб» и «решка». При определении пола
вылупившегося из яйца цыпленка пространство элементарных событий также состоит
из двух элементарных событий:
- «герб» и «решка». При определении пола
вылупившегося из яйца цыпленка пространство элементарных событий также состоит
из двух элементарных событий: 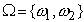 - «самец» и «самка».
- «самец» и «самка».
При бросании кубика с пронумерованными от 1 до 6
гранями (игральная кость) пространство элементарных событий состоит из шести
элементарных событий: 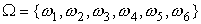 ,
где
,
где 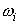 соответствует
номеру грани, которая оказывается после бросания наверху.
соответствует
номеру грани, которая оказывается после бросания наверху.
При определении массы новорожденного элементарными
событиями будут все возможные результаты взвешивания. Количество элементарных
событий в данном случае зависит от возможного диапазона изменения массы и от
точности взвешивания. Часто, однако, в подобных ситуациях удобно расширить
множество элементарных событий, отказавшись от указания диапазона изменения
измеряемой величины и допустив неограниченную точность измерения. В этом случае
множество элементарных событий будет состоять из всех действительных чисел от 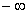 до
до 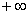 . Конечно, при этом среди
элементарных событий будут такие, которые заведомо не могут появиться в
результате испытания, например, -2 г, 20,5 г, 10100 г и
т. п., однако это не противоречит определению пространства элементарных
событий.
. Конечно, при этом среди
элементарных событий будут такие, которые заведомо не могут появиться в
результате испытания, например, -2 г, 20,5 г, 10100 г и
т. п., однако это не противоречит определению пространства элементарных
событий.
Пространство элементарных событий 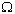 может порождаться не одной, а
двумя и более измеряемыми характеристиками. Например, если одновременно
фиксируется вес и рост новорожденного, то пространство элементарных событий
состоит из пар действительных чисел, т. е. геометрически представляет собой
плоскость.
может порождаться не одной, а
двумя и более измеряемыми характеристиками. Например, если одновременно
фиксируется вес и рост новорожденного, то пространство элементарных событий
состоит из пар действительных чисел, т. е. геометрически представляет собой
плоскость.
1.2. Случайные события и
операции над ними
Элементарные события можно объединять в более
сложные события. Например, объединение элементарных событий 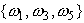 при бросании кубика образует событие «выпадение
нечетного номера». Вообще, любое подмножество пространства элементарных событий
называется случайным (составным) событием, или просто событием.
Событие
при бросании кубика образует событие «выпадение
нечетного номера». Вообще, любое подмножество пространства элементарных событий
называется случайным (составным) событием, или просто событием.
Событие 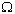 , включающее все элементарные события, называется достоверным
или полным. Считается, что событие происходит, когда происходит
одно из составляющих его элементарных событий. Например, событие
, включающее все элементарные события, называется достоверным
или полным. Считается, что событие происходит, когда происходит
одно из составляющих его элементарных событий. Например, событие 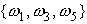 происходит, когда проиходит или
происходит, когда проиходит или 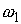 , или
, или 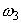 , или
, или
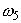 . Полное событие происходит всегда, поскольку в
результате испытания обязательно должно произойти одно из элементарных событий.
Полезно ввести понятие невозможного, или пустого события
. Полное событие происходит всегда, поскольку в
результате испытания обязательно должно произойти одно из элементарных событий.
Полезно ввести понятие невозможного, или пустого события 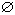 , т. е. события, не
содержащего ни одного элементарного события. Невозможное событие не происходит
никогда.
, т. е. события, не
содержащего ни одного элементарного события. Невозможное событие не происходит
никогда.
Поскольку все события являются множествами
элементарных событий, то их можно комбинировать, используя
теоретико-множественные операции: объединение, пересечение, дополнение.
Операции над событиями
·
Объединением, или суммой событий А и В,
называется событие (обозначается 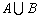 ), состоящее из всех элементарных
событий, входящих хотя бы в одно из событий А или В. Событие
), состоящее из всех элементарных
событий, входящих хотя бы в одно из событий А или В. Событие 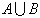 происходит, когда
происходит хотя бы одно из событий А или В.
происходит, когда
происходит хотя бы одно из событий А или В.
·
Пересечением, или произведением событий А и В,
называется событие (обозначается 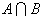 или АВ), состоящее из
всех элементарных событий, входящих одновременно и в A,
и в В. Событие
или АВ), состоящее из
всех элементарных событий, входящих одновременно и в A,
и в В. Событие 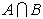 происходит, когда происходят
одновременно А и В.
происходит, когда происходят
одновременно А и В.
·
Дополнением, или отрицанием события А, называется
событие (обозначается 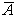 ), включающее все элементарные
события, не входящие в А. Событие
), включающее все элементарные
события, не входящие в А. Событие 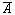 происходит, когда не происходит А.
происходит, когда не происходит А.
События А и В называются непересекающимися,
или несовместными, если их пересечение есть невозможное событие,
т. е. 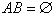 .
.
Будем в дальнейшем обозначать объединение двух
несовместных событий А и В через А+В.
Определение.
Система событий A1,...,Ak называется полной системой событий,
если 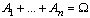 и
и 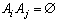 для всех
для всех 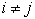 .
.
Примером полной системы будет система всех
элементарных событий 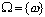 .
Любая пара событий A и
.
Любая пара событий A и 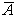 также представляет собой полную систему.
также представляет собой полную систему.
1.3. Вероятности событий
Понятие вероятности имеет два аспекта: содержательный
и формально-математический.
С содержательной точки зрения вероятность некоторого
события определяется относительными шансами появления этого события по
сравнению с другими событиями. Экспериментально эти шансы реализуются при
многократном повторении событий. Частота появления события в длинном ряду
испытаний является естественной оценкой вероятности события.
Точный смысл сказанному помогает дать формальное
аксиоматическое определение вероятности.
Определение.
Для заданного пространства элементарных событий 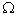 вероятностью
события А называется
функция Р(А), удовлетворяющая следующим аксиомам:
вероятностью
события А называется
функция Р(А), удовлетворяющая следующим аксиомам:
1. 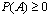 для любого А
для любого А
2. 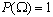
3.
P(A1+A2+...)=P(A1)+P(A2)+....,
если 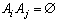 для любых
для любых 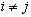 .
.
Из этих аксиом следует, что
1. 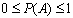 для любого А.
для любого А.
2.
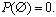
3.
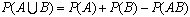
Естественность этих аксиом вытекает из доказываемой
на их основе теоремы Бернулли, связывающей аксиоматическое определение
вероятности с ее частотной интерпретацией.
Теорема Бернулли. Вероятность отклонения частоты появления события А
в п независимых испытаниях (понятие независимости будет введено позднее)
от вероятности этого события Р(А) на величину большую, чем
заданное число 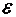 ,
стремится к 0 при п, стремящемся к бесконечности:
,
стремится к 0 при п, стремящемся к бесконечности:
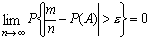
где т - число появлений
события А в п испытаниях.
Эта теорема утверждает, как нам и хотелось бы, что
при увеличении числа испытаний частота стремится к вероятности, однако не в
обычном детерминированном смысле, а в вероятностном. При этом в принципе не
исключается возможность того, что даже при очень большом числе испытаний может
получиться значение частоты т/п, сильно отличающееся от
вероятности Р(А), однако вероятность этого события очень
мала.
Другим доводом в пользу выбранной системы аксиом
будет наличие конкретных вероятностных моделей, в которых эта система аксиом
естественна. Рассмотрим две такие модели.
Классическая модель равновероятных элементарных
событий
В классической модели элементарные события считаются
равновероятными. Например, испытания с бросанием монеты (два равновероятных
события) или кубика (шесть равновероятных событий), результаты скрещивания
гетерозиготных особей Аа (четыре равновероятных события: АА, Аа, аА, аа).
Вероятность события в классической модели
определяется как отношение числа элементарных событий, составляющих это
событие, к числу всех элементарных событий. Например, вероятность получения
потомка с доминантным признаком в результате скрещивания двух гетерозиготных
особей равна 3/4, поскольку это событие включает (часто говорят - «ему
благоприятствуют») три элементарных события (АА, Аа и аА) из
четырех возможных (опыт Менделя).
Очевидно, что свойства вероятности, постулируемые в
аксиоматическом определении, здесь непосредственно следуют из определения
вероятности как отношения числа «благоприятствующих» элементарных событий к
общему числу возможных равновероятных событий.
Решение вероятностных задач с использованием
классической модели часто облегчается использованием комбинаторных формул. Эти
формулы определяют число элементарных событий в некотором опыте, состоящем в
выборе наудачу m элементов
из n различных
элементов. При этом в постановке каждого такого опыта строго оговорено, каким
способом производится выбор и что понимается под различными выборами.
Существуют две принципиально различные схемы выбора.
В первой схеме выбор осуществляется без возвращения элементов, т.е. каждый отобранный
элемент исключается из исходного множества n
элементов. Назовем эту схему – «выбор
без возвращения». Во второй схеме выбор осуществляется поэлементно с
обязательным возвращением отобранного элемента на каждом шаге и тщательным
перемешиванием исходного множества перед следующим выбором. Назовем эту схему –
«выбор с возвращением». После того как выбор осуществлен,
отобранные элементы могут быть либо упорядочены в порядке выбора из исходного
множества (в этом случае будем говорить, что «порядок выбора элементов
важен»), либо нет (в этом случае будем говорить, что «порядок
выбора элементов не важен»).
Следовательно, для определения числа способов
(обозначим это число – N) выбора m элементов из исходного множества n элементов
надо рассмотреть четыре различные постановки задачи:
1. Выбор без возвращения. Порядок выбора важен.
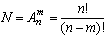
2. Выбор без возвращения. Порядок выбора не важен.
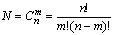
3. Выбор с возвращением. Порядок выбора важен.
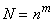
4. Выбор с возвращением. Порядок выбора не важен.
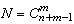
Задачи
1.
Сколькими способами можно
разместить двенадцать мышей, занумерованных от 1 до 12, в четырех клетках A,
B, С, D по три
мыши в каждой?
2.
В распоряжении агрохимика есть
шесть различных типов минеральных удобрений. Ему необходимо провести
эксперименты по изучению совместного влияния любой тройки минеральных
удобрений. Сколько всего экспериментов ему придется провести, если: a) порядок
внесения удобрений несущественен? b) Существенен?
3.
Для лечения
некоторой хронической болезни применяются пять лекарств a, b, c,
d, e. Врач хочет провести сравнительное исследование трех из этих
пяти лекарств. Три исследуемых лекарства врач отбирает из данных пяти случайным
образом. Чему равна вероятность того, что: a) лекарство a будет исследовано? б) будут исследованы лекарства a и b? в) будет исследовано по крайней
мере одно из лекарств a и b?
4.
В некоторой лаборатории
партии животных проверяют выборочно, а именно, партию из десяти животных
принимают, если при проверке трех из них, выбранных наугад, трое оказываются
здоровыми. Какова вероятность того, что лаборатория примет партию животных, в
которой 6 больных животных?
5.
Классифицируются r особей по n признакам, 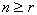 . Найти вероятность того,
что никакие две особи не принадлежат к одному и тому же классу. Все возможные
распределения особей по классам равновероятны.
. Найти вероятность того,
что никакие две особи не принадлежат к одному и тому же классу. Все возможные
распределения особей по классам равновероятны.
6.
“Осторожный фальшивомонетчик”.
Дворцовый чеканщик кладет в каждый ящик вместимостью в сто монет одну
фальшивую. Король подозревает чеканщика и подвергает проверке монеты, взятые
наудачу по одной в каждом из 100 ящиков. Какова вероятность того, что чеканщик
не будет разоблачен?
Геометрическая модель
Рассмотрим некоторую область 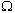 на
плоскости с площадью
на
плоскости с площадью 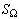 . Определим
вероятность произвольного участка А с площадью Sa в этой области как долю его площади в площади всей
области:
. Определим
вероятность произвольного участка А с площадью Sa в этой области как долю его площади в площади всей
области:
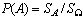
С помощью такой модели можно, например, описать
эксперимент, состоящий в регистрации попадания космической частицы на
фотопластинку.
Определение вероятности в соответствии с приведенной
формулой полностью согласуется с аксиоматическим определением, поскольку из
геометрических свойств площадей непосредственно следует, что 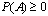 ,
, 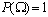 , и Р(А+В)=Р(А)
+Р(В), если
, и Р(А+В)=Р(А)
+Р(В), если 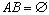 .
.
1.4. Условная вероятность и независимость событий
Условной вероятностью 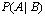 события А при условии, что произошло
событие В, называют отношение
события А при условии, что произошло
событие В, называют отношение
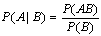
вероятности пересечения событий A
и В к вероятности события В (предполагается, что 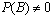 ). Из определения
условной вероятности непосредственно следует правило умножения:
). Из определения
условной вероятности непосредственно следует правило умножения:
Р(АВ)=Р(А|В)Р(В)
Рассматривая условные вероятности при условии В,
мы фактически переходим к новой генеральной совокупности, которая является
частью первоначальной и включает только элементы, соответствующие событию В.
Доля таких элементов в генеральной совокупности равна Р(В).
Событие А|В можно интерпретировать как извлечение элемента, соответствующего
событию А из совокупности элементов, соответствующих событию В.
Доля таких элементов во всей генеральной совокупности равна Р(АВ),
а доля их в В равна Р(АВ)/Р(В).
Пример.
Найдем вероятность того, что потомок, полученный в результате скрещивания
гетерозиготных родителей, гомозиготен, если он имеет доминантный признак.
Вероятность наличия доминантного признака равна, как
мы уже видели, 3/4. Вероятность гомозиготности при наличии доминантного аллеля,
т. е. вероятность пересечения событий {АА, аа} и {АА, Аа, аА},
равна вероятности события АА, т. е. 1/4. Таким образом, искомая условная
вероятность равна
1/4:3/4=1/3
С понятием условной вероятности тесно связано понятие
независимости событий. Вообще, можно определить понятие независимости и
безотносительно к условной вероятности. А именно, два события называются
независимыми, если вероятность их пересечения равна произведению их
вероятностей:
Р(АВ)=Р(А)Р(В)
Из этого определения, однако, сразу следует, что
условная вероятность А при условии В равна безусловной
вероятности А:
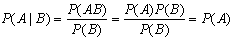
и также, что условная вероятность В при
условии А равна безусловной вероятности В:
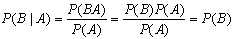
Более того, любое из условий Р(А|В)=Р(А)
или Р(В|А)=Р(В) влечет выполнение соотношения
Р(АВ)=Р(А)Р(В)
определяющего независимость.
Примеры.
1. Рассмотрим два события: А - попадание частицы
в левую половину фотопластинки, В - попадание частицы в нижнюю четверть
фотопластинки. События А и В имеют вероятности 1/2 и 1/4. Событие
АВ, соответствующее попаданию частицы в пересечение А и В,
т.е. в левый нижний угол фотопластинки, имеет вероятность 1/8. Поскольку 1/8=1/2*1/4,
т. е. Р(АВ)=Р(А)Р(В), то
события А и В независимы.
2. Зависимы ли события «наличие доминантного признака» {АА,
Аа, аА} и гомозиготность {АА, аа}? Вероятность первого
события равна 3/4, вероятность второго - 1/2. Вероятность их пересечения равна 1/4.
Поскольку 1/4¹3/4*1/2, то события не являются независимыми.
К этому же
выводу можно прийти иначе. Мы видели, что вероятность гомозиготности при
наличии доминантного аллеля равна 1/3. Вообще же вероятность гомозиготного
потомка равна 1/2. Таким образом, условная вероятность не равна безусловной и,
следовательно, события зависимы.
3. Рассмотрим случайное испытание, состоящее из двух
последовательных бросаний монеты. Результатом этого события будут четыре
равновероятных элементарных события: герб - герб, герб - решка, решка - герб,
решка - решка (или ГГ, ГР, РГ, РР). Зависимы ли события «выпадение герба в
первом бросании» А={ГГ, ГР} и «выпадение герба во втором бросании» В={ГГ,
РГ}? Имеем Р(A)=1/2, Р(B)=1/2, Р(AB)=Р(ГГ)=1/4. Поскольку Р(АВ)=Р(А)Р(В),
то события независимы.
Задачи
1. Два охотника стреляют в волка,
причем каждый делает по одному выстрелу. Для первого охотника вероятность
попадания в цель 0,7, для второго – 0,8. Какова вероятность хотя бы одного
попадания? Как изменится результат, если охотники сделают по два выстрела?
2.
Докажите, что события A и 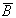 (
(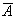 и
и 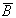 ) независимы, если
независимы A и B?
) независимы, если
независимы A и B?
3.
Докажите, что если два события A и B c положительными
вероятностями несовместны, то они зависимы.
4.
Какова вероятность, что в семье с
двумя детьми оба мальчики, если известно, что в семье уже есть мальчик. Все
возможные распределения детей по полу равновероятны.
5.
Известно, что при трех бросаниях
игральной кости цифра 6 выпала хотя бы один раз. Какова вероятность того, что
она выпала два раза?
6.
Предположим, что в семье с 3-мя
детьми все возможные распределения детей по полу равновероятны. Событие A - «в семье имеются
дети обоих полов» и событие B -
«в семье имеется не более одной девочки». 1) События A
и B независимы? 2) А для семей с 2-мя детьми события A
и B независимы?
1.5. Формула полной
вероятности и формула Байеса
Пусть имеется полная система событий 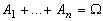 ,
, 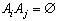 для
для 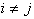 , тогда для любого события В имеем
, тогда для любого события В имеем
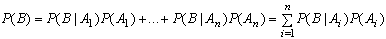
(формула полной
вероятности).
Пример.
Пусть имеются три трудноразличимые при диагнозе болезни а1, А2,
А3, встречающиеся с частотой 50, 40 и 10%, и есть метод
лечения В, приводящий к успеху соответственно в 70, 75 и 90% случаев.
Какова вероятность излечения для пациента, страдающего одной (неизвестно, какой
именно) из болезней а1, А2 или А3?
Имеем P(A1)=0,5; Р(А2)=0,4; Р(A3)=0,1; P(B|A1)=0,7;
Р(В|A2)=0,75;
Р(В|A3)=0,9.
Получаем
Р(В)=0,5*0,7+0,4*0,75+0,1*0,9=0,74
Из соотношений, полученных в соответствии с правилом
умножения
Р(AiB)=Р(В|Ai)Р(Ai) и
Р(AiB)=Р(Ai|В)Р(В)
находим
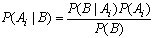
Заменяя Р(В) в знаменателе по формуле
полной вероятности, получаем формулу Байеса, или формулу
вероятностей гипотез
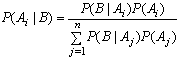
Вероятности P(Ai), i=1,...,n,
в данном контексте носят название априорных вероятностей гипотез Ai, а вероятности P(Ai|B), i=1,...,n, называются апостериорными вероятностями гипотез Ai. Формула
Байеса, таким образом, позволяет, исходя из результатов эксперимента,
корректировать имеющиеся знания о вероятностях интересующих нас событий.
Пример.
Рассмотрим предыдущие данные, однако изменим вопрос. Предположим, что лечение
по методу В оказалось успешным. Что можно сказать на основании этого
факта относительно диагноза? Формула Байеса дает следующие результаты:
P(A1|B)=0,5*0,7/0,74=0,47
P(A2|B)=0,4*0,75/0,74=0,4
P(A3|B)=0,1*0,9/0,74=0,13
Мы видим, что вероятность диагноза А1
несколько снизилась, а вероятность диагноза A3 повысилась, что, конечно, естественно, поскольку
лечение В более эффективно при болезни A3.
Задачи.
1.
Предположим, что 5% всех мужчин и
0,25% всех женщин дальтоники. Наугад выбранное лицо оказалось дальтоником.
Какова вероятность, что это мужчина? (Считать, что мужчин и женщин одинаковое
число.)
2.
При рентгеновском обследовании
вероятность обнаружить заболевание туберкулезом у больного туберкулезом равна 0,9.
Вероятность принять здорового человека за больного равна 0,01. Пусть доля
больных туберкулезом по отношению ко всему населению равна 0,001. Найти
вероятность того, что человек здоров, если он был признан больным при
обследовании.
3. Среди 25 экзаменационных
билетов 5 «хороших». Два студента по очереди берут по одному билету. Найти
вероятности следующих событий: А=(первый студент взял хороший билет); В=(второй
студент взял хороший билет); С=(оба студента взяли хорошие билеты).
4.
Из 10 мышей менее трех доживают
до двух лет с равной вероятностью. Найти вероятность того, что из взятых наугад
пяти мышей ни одна не доживет до двух лет. Хотя бы одна доживет до двух лет.
5.
Ваши друзья могут с равной
вероятностью играть в одну из двух игр. В одной игре используется одна
игральная кость, а в другой – две игральные кости. Счет в любой игре равен
количеству очков, выпавших на одной кости, или на обеих костях вместе. Вы
слышите, что в какой-то игре у них выпало 2 очка. Какова вероятность, что они
играют в игру с одной костью?
6.
В первой урне 8 белых и 2 черных
шара, во второй урне 16 черных шаров. Из каждой урны наудачу извлекли по 1
шару, а затем из этих шаров наудачу взят 1 шар. Найдите вероятность того , что
он белый.
7.
Закон Харди-Вайнберга. В
родительской популяции генотипы АА, Аа, аа встречаются с
частотами 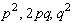 ,
соответственно. Найти распределение генотипов потомков после случайного скрещевания,
т.е. каждого потомока можно рассматриваеть как результат случайного выбора
родителей, и все выборы взаимно независимы.
,
соответственно. Найти распределение генотипов потомков после случайного скрещевания,
т.е. каждого потомока можно рассматриваеть как результат случайного выбора
родителей, и все выборы взаимно независимы.
8.
Найти три вероятности того, что
потомок имеет генотип АA при условии, что одна из
родительских особей (мужская или женская) имеет генотип: (1) АА, (2) Аа,
(3) аа. Другая родительская особь имеет один из генотипов АА, Аа,
аа. В родительской популяции генотипы АА, Аа, аа
встречаются с частотами 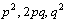 , соответственно, и рассматривается
случайное скрещивание.
, соответственно, и рассматривается
случайное скрещивание.
9.
В родительской популяции генотипы
АА, Аа, аа встречаются с частотами 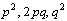 , соответственно. Известно, что их потомок
имеет генотип АA. Найти вероятность того, что его брат имеет генотип Аa
при случайном скрещивании родителей.
, соответственно. Известно, что их потомок
имеет генотип АA. Найти вероятность того, что его брат имеет генотип Аa
при случайном скрещивании родителей.
1.6. Формула Бернулли
При проведении п независимых испытаний, в
каждом из которых вероятность появления события равна р (0<р<1),
вероятность наступления этого события ровно k раз описывается
формулой Бернулли
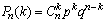
где q=l-p.
Кроме того, вероятность наступления события не менее k1
раз и не более k2
раз (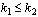 ) равна
) равна
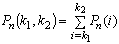
Задачи
1.
Что вероятнее произойдет при
бросании правильной монеты – герб выпадет один раз при двух бросаниях или герб
выпадет три раза при шести бросаниях?
2.
Вероятность хотя бы одного
появления события A при четырех независимых опытах равна 1/2. Какова
вероятность появления события A при одном опыте, если при каждом опыте эта
вероятность одинакова?
3.
Всхожесть семян некоторого сорта
растений оценивается с вероятностью 0,8. Какая вероятность больше, из десяти
наугад выбранных семян взойдет хотя бы одно или из двенадцати семян взойдут
хотя бы два?
4.
В некоторой популяции насекомых 30%
насекомых инфицированы. Что вероятнее, найти хотя бы одну инфицированную особь
из 10 наугад выбранных насекомых или более одной из 12?
5.
При одном цикле осмотра
радиолокационной станции, следящей за космическим объектом, объект будет
обнаружен с вероятностью 0,5. Сколько надо провести циклов осмотра, чтобы
вероятность обнаружения объекта была больше 0,99?

