2. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ РАСПРЕДЕЛЕНИЯ

 

2.1. Случайные величины

Одномерной случайной величиной , или просто случайной величиной, называют любую числовую функцию, определенную на пространстве элементарных событий .

Примеры.

1.       Рассмотрим пространство элементарных событий, которое получается в результате независимых бросаний двух монет. В этом примере пространство элементарных событий состоит из четырех элементарных событий, которым сопоставляется вероятность 1/4. Определим теперь на этом пространстве случайную величину , равную числу гербов, появившихся при бросании двух монет. Очевидно, что значения случайной величины  есть 0, 1, 2, и случайная величина принимает эти значения с вероятностями 0,25, 0,5, 0,25, соответственно.

2.       Пусть у нас имеется некоторое количество кроликов (N), среди которых доля альбиносов равна 0.05. Предположим, что мы из общего количества N кроликов наугад выбрали 40. Рассмотрим пространство элементарных событий  для представления результатов данного эксперимента. В этом примере пространство элементарных событий состоит из 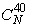 равновероятных элементарных событий. Определим теперь на этом пространстве случайную величину , равную числу альбиносов среди 40 выбранных кроликов. Множество возможных значений случайной величины  есть числа от 0 до 40 включительно. Из формулы Бернулли следует, что вероятность того, что случайная величина  примет значение i, где i=0, 1, 2, ..., 40, равна

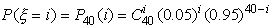
Так как одномерная случайная величина 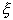 представляет собой числовую функцию на пространстве элементарных событии, то любая числовая функция 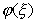 от случайной величины в соответствии с определением также является случайной величиной.

2.2. Функция распределения вероятностей случайной величины

Определение. Функцией распределения вероятностей, или просто функцией распределения (иногда применяют термин кумулятивная функция распределения) случайной величины , называется функция F(х), равная для любого значения x вероятности события :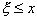

Иногда в литературе применяется другое обозначение функции распределения вероятностей случайной величины .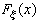

Из определения (2.1) легко вывести свойства функции распределения:

1.      

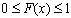
2.       F (х) - неубывающая функция

3.      

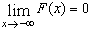
4.        

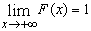
5.      

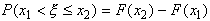
На рис. 2.1 приведен график функции распределения вероятностей случайной величины из первого примера предшествующего пункта.

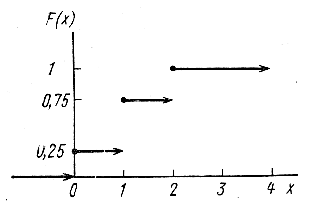
Рис. 2.1. Функция распределения F(x) случайной величины из первого примера 2.1.

 

2.3. Дискретные случайные величины

Различаются два типа случайных величин: дискретные, принимающие конечное или счетное число значений, и непрерывные, принимающие все значения на некотором непрерывном промежутке числовой оси.

Определение. Дискретной случайной величиной 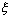 называется случайная величина, принимающая конечное или счетное множество значений х₀, х₁, x₂,... .

Обозначим множество всех возможных значений, которые принимает дискретная случайная величина , через x₀, х₁, х₂,..., а вероятности, с которыми  принимает эти значения, - через р₀, р₁, р₂,... . Тогда 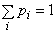. Распределение дискретной случайной величины  будет полностью описано, если указать для любого i вероятность р_i того, что 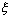 принимает значение x_i, т.е. 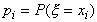. Функция распределения F(x) дискретной случайной величины 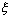 при этом оказывается равной

.

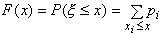Таким образом, F(x) - ступенчатая функция, равная постоянной на любом интервале, не содержащем точек x_i, и имеющая в каждой точке x_i скачок вверх на величину p_i.

Таким образом, чтобы задать дискретную случайную величину , достаточно описать множество всех возможных значений случайной величины x₀, х₁, х₂,..., а также указать числа р_i такие, что

1.                

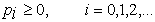
2.                

Наиболее распространенными формами представления дискретных случайных величин являются табличная

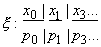
и графическая (рис. 2.2-2.5), отображающие зависимость 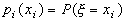 - вероятности р_i от возможного значения случайной величины x_i. Функция 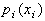, выражающая эту зависимость, называется распределением вероятностей  дискретной случайной величины.

Наиболее известными примерами дискретных случайных величин являются: случайная величина, распределенная по дискретному равномерному закону, биномиально распределенная случайная величина, случайная величина, распределенная по закону Бернулли, случайная  величина, распределенная по закону Пуассона.

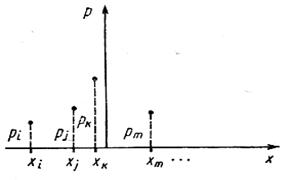
Рис.2.2. Распределение вероятностей дискретной

случайной величины.

 

Случайная величина, принимающая п (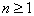) значений х₁, х₂,..., x_n с вероятностями р_i=1/п, называется случайной величиной, распределенной по дискретному равномерному закону. На рис. 2.3 рассматриваемая случайная величина (для n=6) представлена в графической форме. Случайная величина, распределенная по дискретному равномерному закону, является моделью событий с равновероятными исходами (см. пример с бросанием игральной кости).

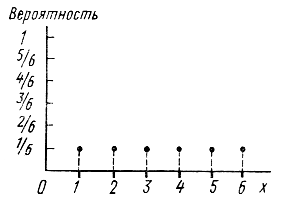
Рис.2.3. Распределение вероятностей дискретного равномерного распределения (n=6).

 

Случайная величина, принимающая два значения: 0 и 1 с вероятностями q=1-р и р, соответственно (0<р<1), называется случайной величиной, распределенной по закону Бернулли с параметром p. Случайная величина, распределенная по закону Бернулли - это удачная модель для описания многих конкретных испытаний, имеющих два исхода (наиболее известный пример - бросание правильной монеты; здесь p=q=1/2), в том числе и в биологии: присутствие или отсутствие некоторого признака: пол родившегося цыпленка, цвет цветка и т. д..

Случайная величина 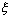, принимающая п+1 значение 0, 1, 2,..., п, с вероятностями

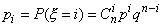
где i=0, 1, 2,..., n, q=1-р, 0<p<1, называется биноминально распределенной случайной величиной, а п и р - параметрами распределения.

На рис. 2.4 биномиальная случайная величина представлена в графической форме. Пример использования биномиальной случайной величины дан в 2.1.

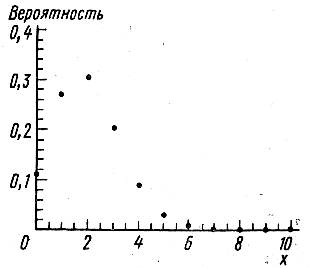
Рис. 2.4. Распределение вероятностей биномиально

распределенной случайной величины для n=10 и p=0.2.

 

Заметим также, что случайная величина, распределенная по закону Бернулли, является частным случаем биномиальной случайной величины для n=1.

Случайная величина 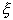, принимающая счетное множество значений 0, 1, 2,..., с вероятностями

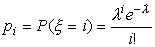
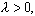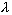где i=0, 1, 2, ...,  называется случайной величиной, распределенной по закону Пуассона. Величина  называется параметром распределения Пуассона.

На рис. 2.5 случайная величина, распределенная по закону Пуассона, представлена в графической форме. Случайная величина, распределенная по закону Пуассона, служит моделью эксперимента, связанного с определением численности бактерий в единице объема, или численности животных на единицу площади, и других подобных экспериментов.

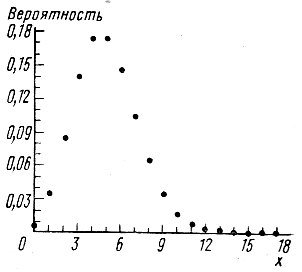
Рис. 2.5. Распределение вероятностей Пуассоновской случайной величины с λ=5.

 

Распределение Пуассона иногда называют "распределением вероятностей редких событий" поскольку оно хорошо описывает ситуацию случайно и независимо друг от друга появляющихся событий  в течение заданного периода времени (регистрации радиоактивных частиц в счетчике Гейгера, телефонные звонки, появление посетителей в малопосещаемом магазине и т.п.).  Существенна именно независимость событий, а их "редкость" требуется лишь для того, чтобы можно было пренебречь вероятностью одновременного появления двух событий. Если параметр 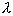 относится к единице времени, то периоду времени длительностью t будет соответствовать пуассоновское распределение с параметром 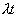. Соответственно, вероятность того, что в течение периода t не произойдет ни одного события равна

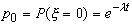
Если, например, появление события влечет гибель организма, то можно 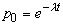интерпретировать как вероятность того, что организм доживет до возраста t. Параметр 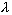 в этом случае называют интенсивностью смертности, или просто смертностью. Из приведенной формулы видно, что  чем больше 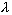, тем меньше вероятность дожить до заданного возраста t и, конечно, чем больше этот заданный возраст, тем меньше вероятность до него дожить (типичный пример - время жизни стакана в столовой).

 

Из других часто используемых дискретных распределений отметим  отрицательное биномиальное распределение и гипергеометрическое распределение.

Задачи

1.     Нарисовать график функции распределения случайной величины, распределенной по закону Бернулли.

2.     Нарисовать график функции распределения случайной величины, распределенной по дискретному равномерному закону (n=6).

3.     Каково должно быть среднее число бактерий в единичной пробе, чтобы вероятность того, что в пробе имеется хотя бы одна бактерия, была не меньше 1/2.

4.     Имеется пять проб воздуха единичного объема, которые в среднем содержат по 2 бактерии в пробе. Найти вероятность того, что по крайней мере в одной пробе имеется не менее двух бактерий.

 

2.4. Непрерывные случайные величины

Определение. Непрерывной случайной величиной называется случайная величина, для которой функция распределения F(x) непрерывна, и существует функция f(x), называемая функцией плотности вероятностей, или просто функцией плотности, определенная для всех  (непрерывная почти всюду за исключением множества, не имеющего конечных предельных точек), такая что

Формула (2.3) с учетом интерпретации величины интеграла как площади представлена графически на рис. 2.6. Справедливы следующие свойства функции плотности:

1.

2.

3.

Рис. 2.6. Связь между функцией распределения F(x) и функцией плотности f(x).

 

Эти свойства объясняют нам, почему функция плотности служит удачной и, следовательно, распространенной формой представления непрерывных случайных величин, являющихся моделью для описания многих экспериментов, связанных с измерением количественных признаков (например, массы животного, длины какой-то части тела, температуры, влажности, урожайности и т. д.).

Действительно, вероятность  того, что случайная величина  примет значение в интервале от x₁ до x₂, вычисляется, исходя из функции плотности (рис. 2.7).

Рис. 2.7. Определение вероятности  попадания случайной величины  в интервал от x₁ до x₂ по функции плотности.

 

Таким образом, по функции плотности легко сравнить вероятности того, что случайная величина примет значение из одного или другого интервала. Знание функции плотности случайной величины  дает полную информацию о непрерывной случайной величине , т. е. знание о ее распределении. Следовательно, можно вводить непрерывные случайные величины, задавая функцию плотности f(x), для которой, естественно, должны выполняться условия (2.4).

Простейшим примером непрерывной случайной величины является равномерно распределенная случайная величина.

Определение. Случайная величина  называется равномерно распределенной на отрезке [a,b] (a и b - это параметры распределения), если ее функция плотности имеет вид

Нетрудно проверить, что так введенная функция удовлетворяет свойствам 2.4. График функции плотности равномерно распределенной на отрезке [a,b] случайной величины приведен на рис. 2.8. Вероятность того, что равномерно распределенная случайная величина  примет значение из отрезка определенной длины, целиком лежащего между a и b, не зависит от расположения этого отрезка. Вероятность принять значения вне отрезка [a,b] равна нулю.

Рис. 2.8. Функция плотности f(x) равномерно распределенной на отрезке [a,b] случайной величины

 

Определение. Непрерывная случайная величина  называется распределенной по экспоненциальному закону с параметром Q если функция плотности f(x) случайной величины  имеет вид

где Q>0.

График функции плотности экспоненциально распределенной случайной величины представлен на рис. 2.9.

Рис. 2.9. Функция плотности f(x) экспоненциального распределения:

(1)  Q=0.2, (2)  Q=0.1

 

Из других часто используемых непрерывных распределений отметим здесь (без определения) треугольное распределение, распределение Эрланга, распределение Вейбулла, гамма-распределение, бета-распределение.

Современные пакеты прикладных программ позволяют получать графики функции распределения, распределения вероятностей дискретной случайной величины и плотности непрерывной случайной величины.

Задачи

1.     Нарисовать график функции распределения случайной величины распределенной по равномерному закону на отрезке [0,1].

2.     Нарисовать график функции распределения случайной величины распределенной по экспоненциальному закону с параметром Q=2.

 

2.5. Нормальное и связанные с ним распределения

Построение статистических моделей чаще всего основывается на предположении о нормальности используемых распределений (иногда применяется термин «гауссовское распределение»).

Определение. Непрерывная случайная величина  называется нормально распределенной случайной величиной (распределенной по нормальному закону) с параметрами  и (записывается ), если функция плотности f(x) случайной величины  имеет вид

где .

График функции плотности нормально распределенной случайной величины представлен на рис. 2.10 в двух вариантах: ,  и , . Заметим, что максимальное значение f(x) достигается при  (), и график f(x) симметричен относительно прямой, проходящей через точку  параллельно оси ординат.

Рис. 2.10. Функция плотности f(x) нормального распределения:

(1)  и , (2)  и

 

При практическом использовании нормального распределения оказывается полезным следующее свойство: площадь под функцией плотности f(x) нормального распределения над интервалом  не зависит от  и  и равна приблизительно 0.68 (k=l); 0.95 (k=1.96); 0.99 (k=2.58), т.е. вероятности нормально распределенной случайной величины принять значение в интервале  равны

Если , то можно доказать, что случайная величина , где а и b - константы. В частности, случайная величина

Это распределение называется стандартным нормальным распределением. Функция плотности f(x) стандартного нормального распределения имеет вид

Многие наблюдаемые в реальных экспериментах случайные величины подчиняются приблизительно нормальному закону распределения. По этой причине значительная часть классической статистической теории предполагает нормальность распределения рассматриваемой случайной величины. Теоретическое основание для этого предположения дает центральная предельная теорема, согласно которой нормированное распределение суммы независимых случайных величин, ни одна из которых не доминирует, при увеличении числа слагаемых сходится к нормальному распределению.

В приложениях статистики очень часто используют связанные с нормальным распределения: распределение (хи-квадрат), распределение Стьюдента (часто применяют обозначение t-распределение) и F-распределение. Плотности этих распределений выражаются через стандартные математические функции в виде некоторых (довольно громозких) формул, которые и служат определением распределений. Мы же дадим «конструктивное» определение, раскрывающее возможности использования этих распределений в математической статистике.

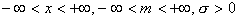Предположим, что каждая из п независимых случайных величин 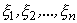 (определение независимости случайных величин будет дано в (4.1) распределена нормально с параметрами 0 и 1 (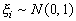). Тогда случайная величина

имеет распределение (хи-квадрат) с п степенями свободы (записывается ).

График функции плотности распределения  изображен на рис. 2.11 в двух вариантах: n=5 и n=10.

Рис. 2.11. Функция плотности -распределения: (1)  n=5 , (2)  n=10.

 

В теории вероятностей дается следующее конструктивное определение распределения Стьюдента.

Предположим, что каждая из п+1 независимых случайных величин  распределена нормально с параметрами 0 и  (). Тогда случайная величина

имеет распределение Стьюдента с п степенями свободы (записывается ).

График функции плотности t-распределения см. на рис. 2.12 в двух вариантах: п=2 и п=10. Заметим, что максимальное значение плотности распределения достигается при х=0, и график симметричен относительно оси ординат.

Рис. 2.12. Функция плотности t -распределения: (1)  n=2 , (2)  n=10.

 

Предположим теперь, что каждая из n+m независимых случайных величин  распределена нормально с параметрами 0 и (. Тогда случайная величина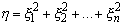

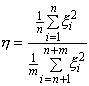
имеет F-распределение с п и т степенями свободы (записывается ).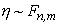

График функции плотности F-распределения представлен на рис. 2.13 в двух вариантах: п=5, m=5 и п=50, m=50.

Рис. 2.13. Функция плотности F -распределения:

(1)  n=5 , m=5; (2) n=50 , m=50.

Иногда возникает ситуация, когда рассматриваемую случайную величину удается с помощью несложных изменений преобразовать в нормально распределенную случайную величину. Так, например, в биологических исследованиях часто возникает логнормальное распределение.

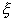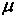Определение. Непрерывная случайная величина  называется распределенной по логнормальному закону с параметрами  и 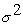, если случайная величина  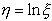распределена нормально ().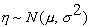